题目内容
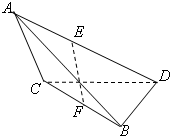 如图,在四面体ABCD中,二面角A-CD-B的平面角为60°,AC⊥CD,BD⊥CD,且AC=CD=2BD,点E、F分别是AD、BC的中点.
如图,在四面体ABCD中,二面角A-CD-B的平面角为60°,AC⊥CD,BD⊥CD,且AC=CD=2BD,点E、F分别是AD、BC的中点.
(Ⅰ)求证:EF⊥平面BCD;
(Ⅱ)求二面角A-BD-C的余弦值.
 (Ⅰ)证明:取DC的中点G,连接EG,FG.
(Ⅰ)证明:取DC的中点G,连接EG,FG.∵点E、F分别是AD、BC的中点.
∴EG,FG分别为△ACD,△BCD的中位线.
故EG⊥CD,FG⊥CD
∵EG∩FG=G.
∴CD⊥平面EFG
∵EF?平面EFG
∴CD⊥EF
可知∠EGF为二面角A-CD-B的平面角,∠EGF=60°.
在△EGF中,EG=2FG,∠EGF=60°,由余弦定理得EF=
 FG,
FG,又由正弦定理得∠EFG=90°
∵GF∩CD=G,GF?面BCD
∴EF⊥平面BCD;
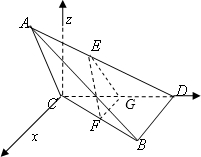
(Ⅱ)解:以C为原点,平面BCD为xoy平面,CD为y轴建立空间直角坐标系.
设BD=1,则C(0,0,0),B(1,2,0),D(0,2,0),A(1,0,
 )
)∴
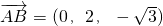 ,
,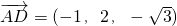 .
.平面BCD的法向量
 =(0,0,1)
=(0,0,1)设平面ABD的法向量
 =(x,y,z),则
=(x,y,z),则 •
• =0,
=0, •
• =0,
=0,∴
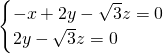 ,∴x=0,
,∴x=0,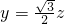 ,
,令z=1,
 =
=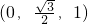
∴
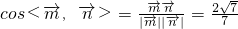
∴二面角A-BD-C的余弦值为
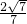 .
.分析:(Ⅰ)取DC的中点G,连接EG,FG,证明CD⊥平面EFG,可得∠EGF为二面角A-CD-B的平面角,在△EGF中,由余弦定理得EF=
 FG,从而可得∠EFG=90°,进而可知EF⊥平面BCD;
FG,从而可得∠EFG=90°,进而可知EF⊥平面BCD;(Ⅱ)建立空间直角坐标系,用坐标表示点与向量,求出平面BCD的法向量
 =(0,0,1),平面ABD的法向量
=(0,0,1),平面ABD的法向量 =
=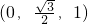 ,利用向量的夹角公式,即可求二面角A-BD-C的余弦值.
,利用向量的夹角公式,即可求二面角A-BD-C的余弦值.点评:本题考查线面垂直,考查面面角,解题的关键是掌握线面垂直的判定方法,正确运用向量法解决面面角问题.

练习册系列答案
相关题目
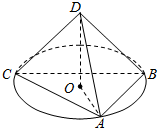 如图,在四面体ABCD中,DA=DB=DC=1,且DA,DB,DC两两互相垂直,点O是△ABC的中心,将△DAO绕直线DO旋转一周,则在旋转过程中,直线DA与BC所成角的余弦值的取值范围是( )
如图,在四面体ABCD中,DA=DB=DC=1,且DA,DB,DC两两互相垂直,点O是△ABC的中心,将△DAO绕直线DO旋转一周,则在旋转过程中,直线DA与BC所成角的余弦值的取值范围是( )A、[0,
| ||||
B、[0,
| ||||
C、[0,
| ||||
D、[0,
|
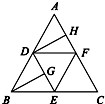 如图,在正三角形ABC中,D,E,F分别为各边的中点,G,H分别为DE,AF的中点,将△ABC沿DE,EF,DF折成正四面体P-DEF,则四面体中异面直线PG与DH所成的角的余弦值为
如图,在正三角形ABC中,D,E,F分别为各边的中点,G,H分别为DE,AF的中点,将△ABC沿DE,EF,DF折成正四面体P-DEF,则四面体中异面直线PG与DH所成的角的余弦值为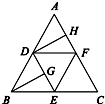 如图,在正三角形ABC中,D,E,F分别为各边的中点,G,H分别为DE,AF的中点,将△ABC沿DE,EF,DF折成正四面体P-DEF,则四面体中异面直线PG与DH所成的角的余弦值为( )
如图,在正三角形ABC中,D,E,F分别为各边的中点,G,H分别为DE,AF的中点,将△ABC沿DE,EF,DF折成正四面体P-DEF,则四面体中异面直线PG与DH所成的角的余弦值为( )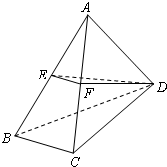 如图,在四面体ABCD中,BC⊥面ACD,DA=DC,E、F分别为AB、AC的中点.
如图,在四面体ABCD中,BC⊥面ACD,DA=DC,E、F分别为AB、AC的中点.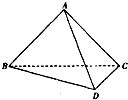 (2009•武汉模拟)如图,在四面体A-BCD中,
(2009•武汉模拟)如图,在四面体A-BCD中,