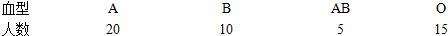题目内容
某高等学校自愿献血的50位学生的血型分布的情况如下表:| 血型 | A | B | AB | O |
| 人数 | 20 | 10 | 5 | 15 |
(Ⅱ)从这50位学生中随机选出2人,求这2人血型相同的概率;
(Ⅲ)现有一位血型为A型的病人需要输血,要从血型为A,O的学生中随机选出2人准备献血,记选出A型血的人数为ξ,求随机变量ξ的分布列及数学期望.
分析:(1)从50位学生中随机选出2人共有C502种结果,这2人血型都为A型有C202种结果,根据古典概型公式得到结果.
(2)从50位学生中随机选出2人共有C502种结果,2人血型相同包括两人都是A型,两人都是B型,两人都是AB型,两人都是O型,根据上面所列的方法,写出结果.
(3)要从血型为A,O的学生中随机选出2人准备献血,选出A型血的人数为ξ,由题意知,变量取0、1、2,分别做出各变量对应的概率,写出分布列,算出期望.
(2)从50位学生中随机选出2人共有C502种结果,2人血型相同包括两人都是A型,两人都是B型,两人都是AB型,两人都是O型,根据上面所列的方法,写出结果.
(3)要从血型为A,O的学生中随机选出2人准备献血,选出A型血的人数为ξ,由题意知,变量取0、1、2,分别做出各变量对应的概率,写出分布列,算出期望.
解答:解:(Ⅰ)记“这2人血型都为A型”为事件A,两个人的血型有C502种结果,这2人血型都为A型有C202种结果,由古典概型公式得P(A)=
=
,即这2人血型都为A型的概率是
.
(Ⅱ)记“这2人血型相同”为事件B,
2人血型相同包括两人都是A型,
两人都是B型,两人都是AB型,两人都是O型,
∴满足条件的事件数是C202+C102+C52+C152,
∴P(B)=
=
=
,
∴这2人血型相同的概率是
.
(Ⅲ)随机变量ξ可能取的值为0,1,2.
且P(ξ=0)=
=
,
P(ξ=1)=
=
,
P(ξ=2)=
=
.
所以ξ的分布列是
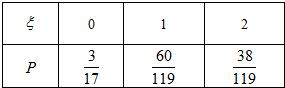
ξ的数学期望为Eξ=0×
+1×
+2×
=
=
.
| ||
|
| 38 |
| 245 |
| 38 |
| 245 |
(Ⅱ)记“这2人血型相同”为事件B,
2人血型相同包括两人都是A型,
两人都是B型,两人都是AB型,两人都是O型,
∴满足条件的事件数是C202+C102+C52+C152,
∴P(B)=
| ||||||||
|
| 350 |
| 1225 |
| 2 |
| 7 |
∴这2人血型相同的概率是
| 2 |
| 7 |
(Ⅲ)随机变量ξ可能取的值为0,1,2.
且P(ξ=0)=
| ||
|
| 3 |
| 17 |
P(ξ=1)=
| ||||
|
| 60 |
| 119 |
P(ξ=2)=
| ||
|
| 38 |
| 119 |
所以ξ的分布列是

ξ的数学期望为Eξ=0×
| 3 |
| 17 |
| 60 |
| 119 |
| 38 |
| 119 |
| 136 |
| 119 |
| 8 |
| 7 |
点评:本小题主要考查古典概型及其概率计算,考查取有限个值的离散型随机变量及其分布列和均值的求法,通过设置密切贴近现实生活的情境,考查概率思想的应用意识和创新意识.这是高考常考的一种题型.

练习册系列答案
相关题目
(09年朝阳区统考)(13分)
某高等学校自愿献血的50位同学的血型分布的情况如下表:
血型 | A | B | AB | O |
人数 | 20 | 10 | 5 | 15 |
(Ⅰ)从这50位同学中随机选出2人,求这2人血型都为A型的概率;
(Ⅱ)从这50位同学中随机选出2人,求这2人血型相同的概率.某高等学校自愿献血的50位学生的血型分布的情况如下表:
|
血型 |
A |
B |
AB |
O |
|
人数 |
20 |
10 |
5 |
15 |
(1) 从这50位学生中随机选出2人,求这2人血型都为A型的概率;
(2)现有一位血型为A型的病人需要输血,要从血型为A,O的学生中随机选出2人准备献血,记选出A型血的人数为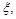 求随机变量
求随机变量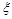 的分布列及数学期望.
的分布列及数学期望.