题目内容
设函数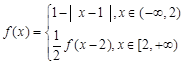 ,则函数
,则函数 的零点的个数为( )
的零点的个数为( )
| A.4 | B.7 | C.6 | D.无穷多个 |
C
解析试题分析: 由题意就是求函数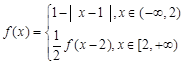 与函数
与函数 交点的个数.作出示意图. 当
交点的个数.作出示意图. 当 时,有一个交点,当
时,有一个交点,当 时,有一个交点
时,有一个交点 ,当
,当 时,由于
时,由于 ,所以有两个交点,当
,所以有两个交点,当 时,由于
时,由于 ,所以有两个交点,当
,所以有两个交点,当 时,由于
时,由于 ,所以没有交点,当
,所以没有交点,当 时,
时, 递减的速度比
递减的速度比 递减(按指数函数
递减(按指数函数 )的速度慢,所以没有交点,因此一共6个交点.
)的速度慢,所以没有交点,因此一共6个交点.
考点:函数图像

练习册系列答案
 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
下列函数是偶函数,且在 上单调递增的是( )
上单调递增的是( )
A. | B. | C. | D. |
函数 的零点是( )
的零点是( )
A. | B. | C. | D. |
若方程 在
在 上有解,则实数
上有解,则实数 的取值范围是( )
的取值范围是( )
A. | B. | C. | D. ∪ ∪ |
设 是定义在R上的奇函数,当
是定义在R上的奇函数,当 ,则
,则 = ( )
= ( )
| A.—3 | B.—1 | C.1 | D.3 |
下列各组函数中,表示同一个函数的是( )
A. 与 与 |
B. 与 与 |
C. 与 与 |
D. 与 与 |
下列函数中,在 内单调递减,并且是偶函数的是( )
内单调递减,并且是偶函数的是( )
A. | B. | C. | D. |
 图象的是( )
图象的是( )
 ,则直线l的方程为( )
,则直线l的方程为( ) x+1
x+1