题目内容
已知两定点A(2,5),B(-2,1),M和N是过原点的直线l上两个动点,且|MN|=2 ,l∥AB,如果直线AM与BN的交点C在y轴上,求M,N及C点的坐标.
,l∥AB,如果直线AM与BN的交点C在y轴上,求M,N及C点的坐标.
答案:
解析:
解析:
|
解 故可设M(a,a),N(b,b),直线AM方程为y-5= ∴AM与y轴交点的纵坐标为 或M(-1,-1),N(1,1),C(0,1). |

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知两定点A(-3,5),B(2,15),动点P在直线3x-4y+4=0上,则|PA|+|PB|的最小值为( )
A、5
| ||
B、
| ||
C、15
| ||
D、5+10
|
 ,由l∥AB且l过原点,得l的方程为y=x,
,由l∥AB且l过原点,得l的方程为y=x, (x-2),
(x-2), ,同理可得BN与y轴交点的纵坐标为
,同理可得BN与y轴交点的纵坐标为 ,得a=-b.又|MN|=2
,得a=-b.又|MN|=2 ,即
,即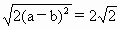 ,解得a=±1,b
,解得a=±1,b 1,∴所求的解为M(1,1),N(-1,-1),C(0,-3)
1,∴所求的解为M(1,1),N(-1,-1),C(0,-3)