题目内容
经过椭圆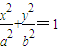 (a>b>0)的右焦点F的直线L与椭圆交于A、B两点,M是线段AB的中点,直线AB与直线OM(O是坐标原点)的斜率分别为k、m,且km=
(a>b>0)的右焦点F的直线L与椭圆交于A、B两点,M是线段AB的中点,直线AB与直线OM(O是坐标原点)的斜率分别为k、m,且km=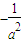 .
.(Ⅰ)求b的值;
(Ⅱ)已知k=
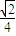 ,连接OM并延长交椭圆于点C,若四边形OACB恰好是平行四边形,求椭圆的方程.
,连接OM并延长交椭圆于点C,若四边形OACB恰好是平行四边形,求椭圆的方程.
【答案】分析:(Ⅰ)设出直线AB的方程代入椭圆方程,利用韦达定理、中点坐标公式,可求m、km,利用km=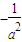 ,即可求b的值;
,即可求b的值;
(Ⅱ)根据OACB是平行四边形,可得 ,从而可求C的坐标,利用C在椭圆上,即可求得椭圆的方程.
,从而可求C的坐标,利用C在椭圆上,即可求得椭圆的方程.
解答:解:(Ⅰ)设直线AB的方程为y=k(x-c),代入椭圆方程,消元可得
(a2k2+b2)x2-2a2k2cx+a2k2c2-a2b2=0,…(2分)
设A(x1,y1),B(x2,y2),M(x,y),则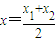 ,m=
,m= ,…(4分)
,…(4分)
∴x= ,y=k(x-c)=-
,y=k(x-c)=-
∴m= =-
=-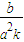 ,∴km=-
,∴km=-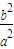 ;
;
又∵km= ,∴b=1; …(6分)
,∴b=1; …(6分)
(Ⅱ)∵OACB是平行四边形,则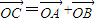 ,…(8分)
,…(8分)
∴xc=x1+x2=2x= =
=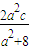 ,yc=y1+y2=2y=
,yc=y1+y2=2y=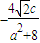 ,
,
∵C在椭圆上,∴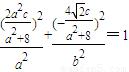 ,…(10分)
,…(10分)
整理得4c2=a2+8,
∵c2=a2-1,∴a2=4,
∴椭圆的方程是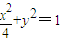 . …(12分)
. …(12分)
点评:本题考查直线与椭圆的位置关系,考查韦达定理的运用,考查向量知识,直线与椭圆联立,利用韦达定理解题是关键.
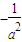 ,即可求b的值;
,即可求b的值;(Ⅱ)根据OACB是平行四边形,可得
 ,从而可求C的坐标,利用C在椭圆上,即可求得椭圆的方程.
,从而可求C的坐标,利用C在椭圆上,即可求得椭圆的方程.解答:解:(Ⅰ)设直线AB的方程为y=k(x-c),代入椭圆方程,消元可得
(a2k2+b2)x2-2a2k2cx+a2k2c2-a2b2=0,…(2分)
设A(x1,y1),B(x2,y2),M(x,y),则
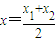 ,m=
,m= ,…(4分)
,…(4分)∴x=
 ,y=k(x-c)=-
,y=k(x-c)=-
∴m=
 =-
=-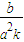 ,∴km=-
,∴km=-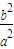 ;
;又∵km=
 ,∴b=1; …(6分)
,∴b=1; …(6分)(Ⅱ)∵OACB是平行四边形,则
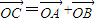 ,…(8分)
,…(8分)∴xc=x1+x2=2x=
 =
=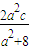 ,yc=y1+y2=2y=
,yc=y1+y2=2y=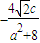 ,
,∵C在椭圆上,∴
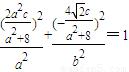 ,…(10分)
,…(10分)整理得4c2=a2+8,
∵c2=a2-1,∴a2=4,
∴椭圆的方程是
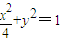 . …(12分)
. …(12分)点评:本题考查直线与椭圆的位置关系,考查韦达定理的运用,考查向量知识,直线与椭圆联立,利用韦达定理解题是关键.

练习册系列答案
相关题目
 y=0经过椭圆
y=0经过椭圆 (a>b>0)的右焦点F及上顶点B,过椭圆外一点(m,0)(m>a)且倾斜角为
(a>b>0)的右焦点F及上顶点B,过椭圆外一点(m,0)(m>a)且倾斜角为 的直线l交椭圆于C,D两点,
的直线l交椭圆于C,D两点, ,求m的取值范围。
,求m的取值范围。 
 如图,已知圆
如图,已知圆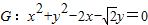 ,经过椭圆
,经过椭圆 (a>b>0)的右焦点F及上顶点B,过椭圆外一点(m,0)(m>a)倾斜角为
(a>b>0)的右焦点F及上顶点B,过椭圆外一点(m,0)(m>a)倾斜角为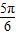 的直线1交椭圆于C,D两点
的直线1交椭圆于C,D两点 如图,已知圆
如图,已知圆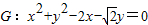 ,经过椭圆
,经过椭圆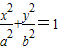 (a>b>0)的右焦点F及上顶点B,过椭圆外一点(m,0)(m>a)倾斜角为
(a>b>0)的右焦点F及上顶点B,过椭圆外一点(m,0)(m>a)倾斜角为 的直线1交椭圆于C,D两点
的直线1交椭圆于C,D两点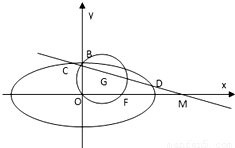 如图,已知圆
如图,已知圆 ,经过椭圆
,经过椭圆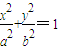 (a>b>0)的右焦点F及上顶点B,过椭圆外一点(m,0)(m>a)倾斜角为
(a>b>0)的右焦点F及上顶点B,过椭圆外一点(m,0)(m>a)倾斜角为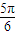 的直线1交椭圆于C,D两点
的直线1交椭圆于C,D两点