题目内容
(1)选修4-2:矩阵与变换二阶矩阵M对应的变换将点(1,-1)与(-2,1)分别变换成点(-1,-1)与(0,-2).
(Ⅰ)求矩阵M的逆矩阵M-1;
(Ⅱ)设直线l在变换M作用下得到了直线m:2x-y=4,求l的方程.
(2)选修4-4:坐标系与参数方程
已知直线的极坐标方程为
 ,圆M的参数方程为
,圆M的参数方程为 (其中θ为参数).
(其中θ为参数).(Ⅰ)将直线的极坐标方程化为直角坐标方程;
(Ⅱ)求圆M上的点到直线的距离的最小值.
(3)选修4一5:不等式选讲
已知函数f(x)=|x-1|+|x+3|.
(Ⅰ)求x的取值范围,使f(x)为常数函数;
(Ⅱ)若关于x的不等式f(x)-a≤0有解,求实数a的取值范围.
【答案】分析:(1)(I) ,由已知二阶矩阵M对应的变换将点(1,-1)与(-2,1)分别变换成点(-1,-1)与(0,-2).可构造关于a,b,c,d的四元一次方程组,解方程组可得矩阵M,进而得到矩阵M的逆矩阵M-1;
,由已知二阶矩阵M对应的变换将点(1,-1)与(-2,1)分别变换成点(-1,-1)与(0,-2).可构造关于a,b,c,d的四元一次方程组,解方程组可得矩阵M,进而得到矩阵M的逆矩阵M-1;
(Ⅱ)由(I)中矩阵M及直线l在变换M作用下得到了直线m:2x-y=4,构造关于x,y的关系式,整理后可得l的方程.
(2)(I)由已知直线的极坐标方程为 ,根据y=ρsinθ,x=ρcosθ可得直线方程,根据圆M的参数方程为
,根据y=ρsinθ,x=ρcosθ可得直线方程,根据圆M的参数方程为 利用三角函数平方关系,消去参数,可得圆的方程.
利用三角函数平方关系,消去参数,可得圆的方程.
(II)根据(I)中所得直线与圆的方程,将圆心坐标及直线方程代入点到直线距离公式,求出圆心到直线的距离,减掉圆半径,可得圆上点到直线的最近距离.
(3)(I)利用零点分段法,可将函数的解析式化为一个分段函数的形式,进而得到f(x)为常数函数时,x的取值范围
(II)分析函数的值域,进而根据关于x的不等式f(x)-a≤0有解,a不小于函数最大值,可得答案.
解答:(1)(本小题满分7分)选修4-2:矩阵与变换
解:(Ⅰ)设 ,则有
,则有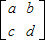
 =
= ,
,
 =
= ,
,
所以 ,
,
解得
所以M= ,从而|M|=-2,
,从而|M|=-2,
从而M-1=
(Ⅱ)因为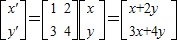
且m:2x'-y'=4,所以2(x+2y)-(3x+4y)=4,
即x+4=0,这就是直线l的方程
(2)(本小题满分7分)选修4-4:坐标系与参数方程
解:(Ⅰ)∵
∴ ,∴ρsinθ+ρcosθ=1.
,∴ρsinθ+ρcosθ=1.
所以,该直线的直角坐标方程为:x+y-1=0.
(Ⅱ)圆M的普通方程为:x2+(y+2)2=4
圆心M(0,-2)到直线x+y-1=0的距离d= .
.
所以,圆M上的点到直线的距离的最小值为 -2.
-2.
(3)(本小题满分7分) 选修4一5:不等式选讲
解:(Ⅰ)f(x)=|x-1|+|x+3|=
则当x∈[-3,1]时,f(x)为常函数.
(Ⅱ)法一:画图,由(1)得函数f(x)的最小值为4,
法二:|x-1|+|x+3|≥|x-1-(x+3)|;
∴|x-1|+|x+3|≥4,
等号当且仅当x∈[-3,1]时成立.
得函数f(x)的最小值为4,则实数a的取值范围为a≥4.
点评:本题是选修三选一,(1)的关键是熟练掌握矩阵运算公式,(2)的关系是将极坐标方程和参数方程转化为一般方程,(3)的关键是用零点分段法,化简函数的解析式.
 ,由已知二阶矩阵M对应的变换将点(1,-1)与(-2,1)分别变换成点(-1,-1)与(0,-2).可构造关于a,b,c,d的四元一次方程组,解方程组可得矩阵M,进而得到矩阵M的逆矩阵M-1;
,由已知二阶矩阵M对应的变换将点(1,-1)与(-2,1)分别变换成点(-1,-1)与(0,-2).可构造关于a,b,c,d的四元一次方程组,解方程组可得矩阵M,进而得到矩阵M的逆矩阵M-1;(Ⅱ)由(I)中矩阵M及直线l在变换M作用下得到了直线m:2x-y=4,构造关于x,y的关系式,整理后可得l的方程.
(2)(I)由已知直线的极坐标方程为
 ,根据y=ρsinθ,x=ρcosθ可得直线方程,根据圆M的参数方程为
,根据y=ρsinθ,x=ρcosθ可得直线方程,根据圆M的参数方程为 利用三角函数平方关系,消去参数,可得圆的方程.
利用三角函数平方关系,消去参数,可得圆的方程.(II)根据(I)中所得直线与圆的方程,将圆心坐标及直线方程代入点到直线距离公式,求出圆心到直线的距离,减掉圆半径,可得圆上点到直线的最近距离.
(3)(I)利用零点分段法,可将函数的解析式化为一个分段函数的形式,进而得到f(x)为常数函数时,x的取值范围
(II)分析函数的值域,进而根据关于x的不等式f(x)-a≤0有解,a不小于函数最大值,可得答案.
解答:(1)(本小题满分7分)选修4-2:矩阵与变换
解:(Ⅰ)设
 ,则有
,则有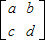
 =
= ,
,
 =
= ,
,所以
 ,
,解得

所以M=
 ,从而|M|=-2,
,从而|M|=-2,从而M-1=

(Ⅱ)因为
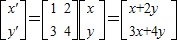
且m:2x'-y'=4,所以2(x+2y)-(3x+4y)=4,
即x+4=0,这就是直线l的方程
(2)(本小题满分7分)选修4-4:坐标系与参数方程
解:(Ⅰ)∵

∴
 ,∴ρsinθ+ρcosθ=1.
,∴ρsinθ+ρcosθ=1.所以,该直线的直角坐标方程为:x+y-1=0.
(Ⅱ)圆M的普通方程为:x2+(y+2)2=4
圆心M(0,-2)到直线x+y-1=0的距离d=
 .
.所以,圆M上的点到直线的距离的最小值为
 -2.
-2.(3)(本小题满分7分) 选修4一5:不等式选讲
解:(Ⅰ)f(x)=|x-1|+|x+3|=

则当x∈[-3,1]时,f(x)为常函数.
(Ⅱ)法一:画图,由(1)得函数f(x)的最小值为4,
法二:|x-1|+|x+3|≥|x-1-(x+3)|;
∴|x-1|+|x+3|≥4,
等号当且仅当x∈[-3,1]时成立.
得函数f(x)的最小值为4,则实数a的取值范围为a≥4.
点评:本题是选修三选一,(1)的关键是熟练掌握矩阵运算公式,(2)的关系是将极坐标方程和参数方程转化为一般方程,(3)的关键是用零点分段法,化简函数的解析式.

练习册系列答案
相关题目
 如图,△ABC是⊙O的内接三角形,PA是⊙O的切线,PB交AC于点E,交⊙O于点D,若PE=PA,
如图,△ABC是⊙O的内接三角形,PA是⊙O的切线,PB交AC于点E,交⊙O于点D,若PE=PA, ,PD=1,BD=8,求线段BC的长.
,PD=1,BD=8,求线段BC的长. ,矩阵阵
,矩阵阵 ,
, ,求在矩阵
,求在矩阵 作用下变换所得到的图形的面积.
作用下变换所得到的图形的面积. (
( 为参数,
为参数, 为常数且
为常数且 )被以原点为极点,
)被以原点为极点, 轴的正半轴为极轴,方程为
轴的正半轴为极轴,方程为 的曲线所截,求截得的弦长.
的曲线所截,求截得的弦长. ,求证:
,求证: .
.