题目内容
(本题是选做题,满分28分,请在下面四个题目中选两个作答,每小题14分,多做按前两题给分)
A.(选修4-1:几何证明选讲)
 如图,△ABC是⊙O的内接三角形,PA是⊙O的切线,PB交AC于点E,交⊙O于点D,若PE=PA,
如图,△ABC是⊙O的内接三角形,PA是⊙O的切线,PB交AC于点E,交⊙O于点D,若PE=PA, ,PD=1,BD=8,求线段BC的长.
,PD=1,BD=8,求线段BC的长.
B.(选修4-2:矩阵与变换)
在直角坐标系中,已知椭圆 ,矩阵阵
,矩阵阵 ,
, ,求在矩阵
,求在矩阵 作用下变换所得到的图形的面积.
作用下变换所得到的图形的面积.
C.(选修4-4:坐标系与参数方程)
直线 (
( 为参数,
为参数, 为常数且
为常数且 )被以原点为极点,
)被以原点为极点, 轴的正半轴为极轴,方程为
轴的正半轴为极轴,方程为 的曲线所截,求截得的弦长.
的曲线所截,求截得的弦长.
D.(选修4-5:不等式选讲)
设 ,求证:
,求证: .
.
A. 由切割线定理得 PA=3, ………………3分
根据弦切角定理 得 , ………………4分
, ………………4分
又因为 PA=PE,所以PA=PE=AE=3,ED=2,BE=6, ………8分
由相交弦定理得 EC=4, ………………10分
在三角形BEC中,根据余弦定理的BC= . ………………14分
. ………………14分
B.
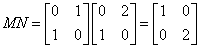 ,
………………4分
,
………………4分
设 为椭圆
为椭圆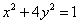 上任一点,它在
上任一点,它在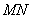 的作用下所对应的点为
的作用下所对应的点为 ,则
,则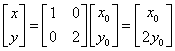 ,
………………6分
,
………………6分
∴ 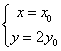 ,即
,即 ,
………………10分
,
………………10分
代入 得
得 ,
………………12分
,
………………12分
∴  .
………………14分
.
………………14分
C.
直线的普通方程为: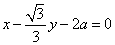 ,
………………4分
,
………………4分
圆的普通方程为: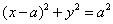 ,
………………8分
,
………………8分
圆心到直线的距离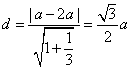 , ………………12分
, ………………12分
∴ 弦长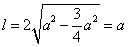 .
………………14分
.
………………14分
D.
 ………………2分
………………2分

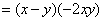 ,
………………8分
,
………………8分
∵ 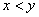 , ∴
, ∴ 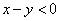 ,
,
又 ,
, , ∴
, ∴ ,
,
∴  ,
………………12分
,
………………12分
∴  .
………………14分
.
………………14分

 (选做题)本题包括A、B、C、D四小题,请选定其中两题,并在答题卡指定区域内作答,若多做,则按作答的前两题评分,解答时应写出文字说明、证明过程或演算步骤.
(选做题)本题包括A、B、C、D四小题,请选定其中两题,并在答题卡指定区域内作答,若多做,则按作答的前两题评分,解答时应写出文字说明、证明过程或演算步骤. (2013•宿迁一模)【选做题】本题包括A、B、C、D四小题,请选定其中两题,并在相应的答题区域内作答.若多做,则按作答的前两题评分.解答时应写出文字说明、证明过程或演算步骤.
(2013•宿迁一模)【选做题】本题包括A、B、C、D四小题,请选定其中两题,并在相应的答题区域内作答.若多做,则按作答的前两题评分.解答时应写出文字说明、证明过程或演算步骤.
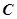 是内接于⊙O,
是内接于⊙O,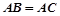 ,直线
,直线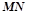 切⊙O于点
切⊙O于点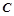 ,弦
,弦 ,
,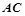 与
与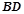 相交于点
相交于点 .
.
 ≌Δ
≌Δ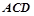 ;
;
 ,求
,求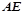 .
.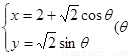 为参数),且曲线C与直线
为参数),且曲线C与直线 =0相交于两点A、B求弦AB的长。
=0相交于两点A、B求弦AB的长。 的一个特征值为
的一个特征值为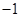 ,它对应的一个特征向量
,它对应的一个特征向量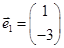 。
。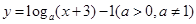 的图象恒过定点
的图象恒过定点 ,若点
,若点 线
线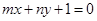 上,其中
上,其中 ,求
,求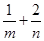 的最小值。
的最小值。