题目内容
设函数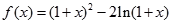 。
。
(Ⅰ)若在定义域内存在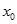 ,使不等式
,使不等式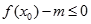 能成立,求实数
能成立,求实数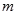 的最小值;
的最小值;
(Ⅱ)若函数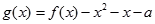 在区间
在区间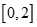 上恰有两个不同的零点,求实数
上恰有两个不同的零点,求实数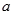 的取值范围。
的取值范围。
(1)1;(2)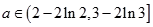
解析试题分析:(1)不等式转化为: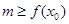 能成立,求m最小值。可以转化成求函数
能成立,求m最小值。可以转化成求函数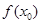 在定义域内的最小值。(2)函数
在定义域内的最小值。(2)函数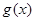 在
在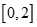 上有两个不同零点,所以
上有两个不同零点,所以 在
在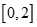 上有两个不同的解,可以令
上有两个不同的解,可以令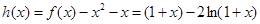 ,结合图形研究函数
,结合图形研究函数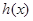 的性质即可。
的性质即可。
解答过程:(Ⅰ)要使得不等式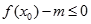 能成立,只需
能成立,只需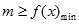 。 ………………1分
。 ………………1分
求导得: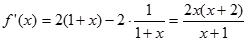 ,…………………………………2分
,…………………………………2分
∵函数 的定义域为
的定义域为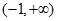 , ……………………………………3分
, ……………………………………3分
当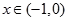 时,
时, ,∴函数
,∴函数 在区间
在区间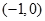 上是减函数;
上是减函数;
当 时,
时, ,∴函数
,∴函数 在区间(0,+∞)上是增函数。 …………5分
在区间(0,+∞)上是增函数。 …………5分
∴ , ∴
, ∴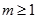 。故实数
。故实数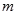 的最小值为1。……………………6分(Ⅱ)由
的最小值为1。……………………6分(Ⅱ)由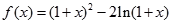 得:
得: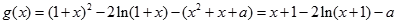 …………………7分
…………………7分
由题设可得:方程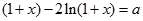 在区间
在区间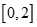 上恰有两个相异实根。
上恰有两个相异实根。
设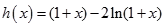 。∵
。∵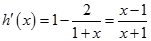 ,列表如下:
,列表如下: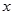
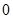
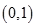
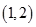
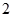
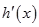
- 0 + 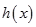
减函数  练习册系列答案
练习册系列答案

名师金考卷系列答案


同步特训小博士系列答案
名师特攻冲刺100分系列答案
金榜一号同步单元全程达标测试AB卷系列答案
亮点激活3加1大试卷系列答案
同步跟踪全程检测系列答案
通城学典课时新体验系列答案
相关题目
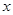 均有
均有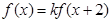 ,其中常数k为负数,且
,其中常数k为负数,且 在区间
在区间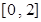 上有表达式
上有表达式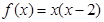
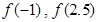 的值;
的值;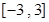 上的表达式,并讨论函数
上的表达式,并讨论函数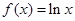 ,
, ,设
,设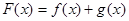 .
.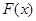 的单调区间;
的单调区间;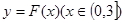 图象上任意一点
图象上任意一点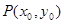 为切点的切线的斜率
为切点的切线的斜率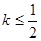
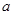 的最小值.
的最小值. ,使得函数
,使得函数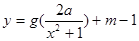 的图象与
的图象与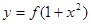 的图
的图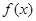 在定义域上是奇函数,且在
在定义域上是奇函数,且在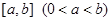 上是减函数,图像如图所示.
上是减函数,图像如图所示.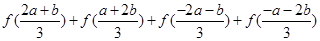 ;
; 上的图像;
上的图像;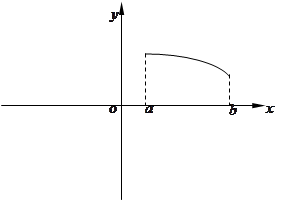
 .
. 在
在 上是单调递增函数;
上是单调递增函数; 时,求函数在
时,求函数在 上的最值;
上的最值; 上恒有
上恒有 成立,求
成立,求 的取值范围.
的取值范围.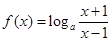 (
(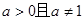 ).
).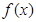 的奇偶性,并证明;
的奇偶性,并证明;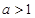 ,用单调性定义证明函数
,用单调性定义证明函数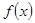 在区间
在区间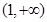 上单调递减;
上单调递减; ,使得
,使得 时,值域为
时,值域为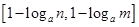 ,若存在,求出实数
,若存在,求出实数 为奇函数;
为奇函数; 以及m的值;
以及m的值; 的图象;
的图象;
 有三个零点,求实数k的取值范围.
有三个零点,求实数k的取值范围.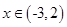 ,求函数
,求函数 =
=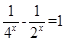 的最大值与最小值.
的最大值与最小值.