题目内容
某校的学生记者团由理科组和文科组构成,具体数据如下表所示:| 组别 | 理科 | 文科 | ||
| 性别 | 男生 | 女生 | 男生 | 女生 |
| 人数 | 5 | 4 | 3 | 2 |
(1)求理科组恰好记4分的概率?
(2)设文科男生被选出的人数为ξ,求随机变量ξ的分布列和数学期望Eξ.
分析:(Ⅰ)由题意知本题符合古典概型,写出试验发生包含的基本事件数,写出满足条件的A为“在理科组选出2名男生、1名女生或选出2名女生”包含的事件数,根据古典概型公式得到结果.
(2)文科男生被选出的人数为ξ,由题意得ξ=0,1,2,3,看出变量对应的事件,根据古典概型公式得到概率,写出分布列,求出期望.
(2)文科男生被选出的人数为ξ,由题意得ξ=0,1,2,3,看出变量对应的事件,根据古典概型公式得到概率,写出分布列,求出期望.
解答:解:(Ⅰ)由题意知本题符合古典概型,
记“理科组恰好记(4分)”的事件为A,
试验发生包含的基本事件数为C93•C51+C92•C52+C91•C53=870
而满足条件的A为“在理科组选出2名男生、1名女生或选出2名女生”共有C52•C41•C51+C42•C52=260种选法,
根据古典概型公式得到
∴P(A)=
=
(Ⅱ)由题意得ξ=0,1,2,3,
∴P(ξ=0)=
,
P(ξ=1)=
,
P(ξ=2)=
,P(ξ=3)=
,
∴ξ的分布列为

∴ξ的数学期望为E(ξ)=0×
+1×
+2×
+3×
=
记“理科组恰好记(4分)”的事件为A,
试验发生包含的基本事件数为C93•C51+C92•C52+C91•C53=870
而满足条件的A为“在理科组选出2名男生、1名女生或选出2名女生”共有C52•C41•C51+C42•C52=260种选法,
根据古典概型公式得到
∴P(A)=
| 260 |
| 870 |
| 26 |
| 87 |
(Ⅱ)由题意得ξ=0,1,2,3,
∴P(ξ=0)=
| 204 |
| 870 |
P(ξ=1)=
| 495 |
| 870 |
P(ξ=2)=
| 162 |
| 870 |
| 9 |
| 870 |
∴ξ的分布列为

∴ξ的数学期望为E(ξ)=0×
| 204 |
| 870 |
| 495 |
| 870 |
| 162 |
| 870 |
| 9 |
| 870 |
| 141 |
| 145 |
点评:本题考查古典概型和离散型随机变量的分布列,本题这种类型是近几年高考题中经常出现的,考查离散型随机变量的分布列和期望,大型考试中理科考试必出的一道问题.

练习册系列答案
相关题目
某校的学生记者团由理科组和文科组构成,具体数据如下表所示:
|
组别 |
理科 |
文科 |
||
|
性别 |
男生 |
女生 |
男生 |
女生 |
|
人数 |
4 |
4 |
3 |
1 |
学校准备从中选出4人到社区举行的大型公益活动进行采访,每选出一名男生,给其所在小组记1分,每选出一名女生则给其所在小组记2分,若要求被选出的4人中理科组、文科组的学生都有.(Ⅰ)求理科组恰好记4分的概率?(4分)
(Ⅱ)设文科男生被选出的人数为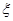 ,求随机变量
,求随机变量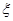 的分布列和数学期望
的分布列和数学期望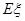 .(8分)
.(8分)
某校的学生记者团由理科组和文科组构成,具体数据如下表所示:
| 组别 | 理科 | 文科 | ||
| 性别 | 男生 | 女生 | 男生 | 女生 |
| 人数 | 5 | 4 | 3 | 2 |
(1)求理科组恰好记4分的概率?
(2)设文科男生被选出的人数为ξ,求随机变量ξ的分布列和数学期望Eξ.
某校的学生记者团由理科组和文科组构成,具体数据如下表所示:
学校准备从中选出4人到社区举行的大型公益活动进行采访,每选出一名男生,给其所在小组记1分,每选出一名女生则给其所在小组记2分,若要求被选出的4人中理科组、文科组的学生都有.
(1)求理科组恰好记4分的概率?
(2)设文科男生被选出的人数为ξ,求随机变量ξ的分布列和数学期望Eξ.
| 组别 | 理科 | 文科 | ||
| 性别 | 男生 | 女生 | 男生 | 女生 |
| 人数 | 5 | 4 | 3 | 2 |
(1)求理科组恰好记4分的概率?
(2)设文科男生被选出的人数为ξ,求随机变量ξ的分布列和数学期望Eξ.
某校的学生记者团由理科组和文科组构成,具体数据如下表所示:
学校准备从中选出4人到社区举行的大型公益活动进行采访,每选出一名男生,给其所在小组记1分,每选出一名女生则给其所在小组记2分,若要求被选出的4人中理科组、文科组的学生都有.
(1)求理科组恰好记4分的概率?
(2)设文科男生被选出的人数为ξ,求随机变量ξ的分布列和数学期望Eξ.
| 组别 | 理科 | 文科 | ||
| 性别 | 男生 | 女生 | 男生 | 女生 |
| 人数 | 5 | 4 | 3 | 2 |
(1)求理科组恰好记4分的概率?
(2)设文科男生被选出的人数为ξ,求随机变量ξ的分布列和数学期望Eξ.