题目内容
(满分13分)已知各项均为正数的数列 是数列
是数列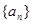 的前n项和,对任意
的前n项和,对任意 ,有2Sn=2
,有2Sn=2 .
.
(Ⅰ)求常数p的值;
(Ⅱ)求数列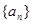 的通项公式;
的通项公式;
(Ⅲ)记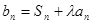 ,(
,( )若数列
)若数列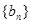 从第二项起每一项都比它的前一项大,求
从第二项起每一项都比它的前一项大,求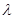 的取值范围.
的取值范围.
【答案】
(1) ;(2)
;(2)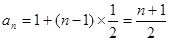 ;(3)
;(3)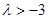 .
.
【解析】
试题分析:(1)由 及
及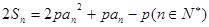 ,得:
,得:
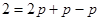
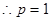
(2)由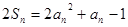 ①
①
得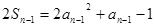 (
(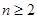 ,
, ) ②
) ②
由②—①,得 
即:
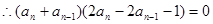
由于数列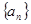 各项均为正数,
各项均为正数,
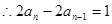 即
即  (
(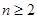 ,
, )
)
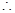 数列
数列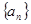 是首项为
是首项为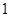 ,公差为
,公差为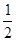 的等差数列,
的等差数列,
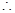 数列
数列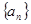 的通项公式是
的通项公式是 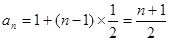
(3)由题意,数列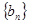 是递增的,
是递增的,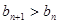 ,即
,即
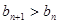 对
对 恒成立,
恒成立,
(2)可得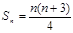 ,
,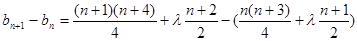 >0恒成立,化简成
>0恒成立,化简成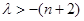 恒成立,得
恒成立,得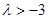 .
.
考点:本题考查了数列通项公式的求法及数列的单调性
点评:关于数列方面的命题主要有以下三个方面:(1)数列本身的有关知识,其中有等差数列、等比数列的概念、性质、通项公式及求和公式;(2)数列与其他知识结合,其中有数列与函数、方程、不等式、三角、几何的结合以及探索性问题

练习册系列答案
相关题目
(本小题满分13分)某厂用甲、乙两种产品,已知生产1吨A产品,1吨B产品分别需要的甲乙原料数、可获得的利润及该厂现有原料数如表:
产品 所需原料 | A产品(t) | B产品(t) | 现有原料(t) |
甲(t) | 2 | 1 | 14 |
乙(t) | 1 | 3 | 18 |
利润(万元) | 5 | 3 |
|
(1)在现有原料下,A、B产品应各生产多少才能使利润最大?
(2)如果1吨B产品的利润增加到20万元,原来的最优解为何改变?
(3)如果1吨B产品的利润减少1万元,原来的最优解为何改变?
(4)1吨B产品的利润在什么范围,原最优解才不会改变?
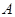 地和
地和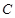 地同时开出,如下图,各沿箭头方向(两方向垂直)匀速前进,汽车和自行车的速度分别是10米/秒和5米/秒,已知
地同时开出,如下图,各沿箭头方向(两方向垂直)匀速前进,汽车和自行车的速度分别是10米/秒和5米/秒,已知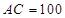 米.(汽车开到
米.(汽车开到
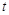 秒后,汽车到达
秒后,汽车到达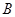 处,自行车到达
处,自行车到达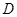 处,设
处,设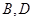 间距离为
间距离为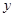 ,试
,试 在区间
在区间 ,
, 内各有一个极值点.
内各有一个极值点. 的最大值;
的最大值; 时,设函数
时,设函数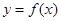 在点
在点 处的切线为
处的切线为 ,若
,若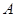 处穿过函数
处穿过函数 的表达式.
的表达式.