题目内容
某地方政府准备在一块面积足够大的荒地上建一如图所示的一个矩形综合性休闲广场,其总面积为3000平方米,其中场地四周(阴影部分)为通道,通道宽度均为2米,中间的三个矩形区域将铺设塑胶地面作为运动场地(其中两个小场地形状相同),塑胶运动场地占地面积为S平方米.
(1)分别写出用x表示y和S的函数关系式(写出函数定义域);
(2)怎样设计能使S取得最大值,最大值为多少?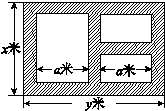
(1)y= (6<x<500).S=3030-
(6<x<500).S=3030-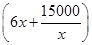 ,6<x<500.
,6<x<500.
(2)x=50 m,y=60 m时,最大面积是2430 m2.
解析试题分析:(1)解实际问题应用题,关键正确理解题意,列出函数关系式,注意交代定义域. 由已知xy=3000,2a+6=y∴x>6,y>6,故y= ,由y>6,解得x<500,∴y=
,由y>6,解得x<500,∴y= (6<x<500).S=(x-4)a+(x-6)a=(2x-10)a,根据2a+6=y,得a=
(6<x<500).S=(x-4)a+(x-6)a=(2x-10)a,根据2a+6=y,得a= -3=
-3=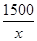 -3,∴S=(2x-10)
-3,∴S=(2x-10)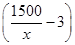 =3030-
=3030-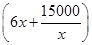 ,6<x<500.(2)由基本不等式求最值,注意等于号取值情况.S=3030-
,6<x<500.(2)由基本不等式求最值,注意等于号取值情况.S=3030-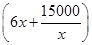 ≤3030-2
≤3030-2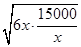 =3030-2×300=2430,当且仅当6x=
=3030-2×300=2430,当且仅当6x= ,即x=50时等号成立,此时y=60.
,即x=50时等号成立,此时y=60.
解:(1)由已知xy=3000,2a+6=y∴x>6,y>6,故y= ,
,
由y>6,解得x<500,∴y= (6<x<500).
(6<x<500).
S=(x-4)a+(x-6)a=(2x-10)a,
根据2a+6=y,得a= -3=
-3=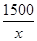 -3,
-3,
∴S=(2x-10)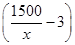 =3030-
=3030-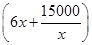 ,6<x<500.
,6<x<500.
(2)S=3030-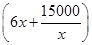 ≤3030-2
≤3030-2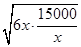 =3030-2×300=2430,
=3030-2×300=2430,
当且仅当6x= ,即x=50时等号成立,此时y=60.
,即x=50时等号成立,此时y=60.
所以,矩形场地x=50 m,y=60 m时,运动场的面积最大,最大面积是2430 m2.
考点:函数应用题,基本不等式求最值

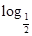 24)的值.
24)的值. 中,
中, 为奇数,
为奇数, 均为整数,且
均为整数,且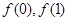 均为奇数.求证:
均为奇数.求证: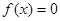 无整数根。
无整数根。 的三内角分别为
的三内角分别为 ,向量
,向量

 ,记函数
,记函数 .
.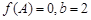 ,求
,求 的方程
的方程 有两个不同的实数解,求实数
有两个不同的实数解,求实数 的取值范围.
的取值范围. km.D为海湾一侧海岸线CT上的一点,设CD=x(km),点D对跑道AB的视角为q.
km.D为海湾一侧海岸线CT上的一点,设CD=x(km),点D对跑道AB的视角为q.

 的图象切x轴于点(2,0),求a、b的值;
的图象切x轴于点(2,0),求a、b的值;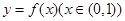 的图象上任意一点的切线斜率为k,试求
的图象上任意一点的切线斜率为k,试求 的充要条件;
的充要条件; .
.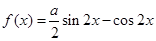 的图象过点
的图象过点 .
. 的值;
的值;  的最小正周期及最大值.
的最小正周期及最大值. 是实数,函数
是实数,函数 (
( ).
). 不是奇函数;
不是奇函数; 时,求满足
时,求满足 的
的 的取值范围;
的取值范围; 的值域(用
的值域(用
 的单调区间.
的单调区间. 有4个不同的实根,求
有4个不同的实根,求 的范围?
的范围? ,使得关于
,使得关于 的方程
的方程 有两个不相等的实根?如果存在,求b
有两个不相等的实根?如果存在,求b