Question

11、方程|x²-2x-3|=a有三解，则a=

4

．

Answer 1

分析：将方程|x²-2x-3|=a有三解，转化成函数y=|x²-2x-3|与y=a有三个交点，结合函数图象观察何时有三个交点即可．

解答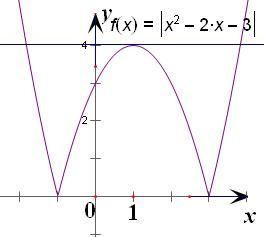：解：方程|x²-2x-3|=a有三解，
可转化成函数y=|x²-2x-3|与y=a有三个交点
画出函数y=|x²-2x-3|
观察图象当a=4时满足条件．

点评：本题主要考查了函数与方程的综合运用，以及绝对值函数的图象，属于基础题．