题目内容
(本小题12分)
已知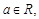 函数
函数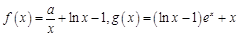
(1)判断函数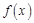 在
在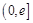 上的单调性;
上的单调性;
(2)是否存在实数 ,使曲线
,使曲线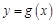 在点
在点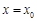 处的切线与
处的切线与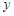 轴垂直?若存在,求出
轴垂直?若存在,求出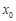 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
【答案】
(1)见解析;(2) 不存在
【解析】(1)先求出 ,然后再分
,然后再分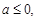
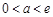 和
和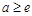 三种情况研究其在区间
三种情况研究其在区间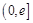 上的单调性.
上的单调性.
(2)本小题所给条件曲线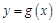 在点
在点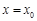 处的切线与
处的切线与 轴垂直实质是研究方程
轴垂直实质是研究方程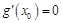 有实数解.然后利用导数研其单调性和最值,画出图像从图像上可分析判断是否有实数解.
有实数解.然后利用导数研其单调性和最值,画出图像从图像上可分析判断是否有实数解.
解;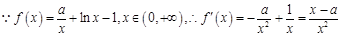
①若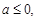 则
则 ,
,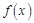 在
在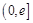 上单调递增
上单调递增
②若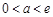 ,当
,当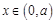 时,
时,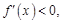 函数
函数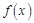 在区间
在区间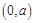 上单调递减,
上单调递减,
当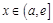 时,
时,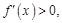 函数
函数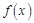 在区间
在区间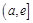 上单调递增
上单调递增
③若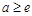 ,则
,则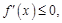 函数
函数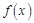 在区间
在区间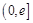 上单调递减.
上单调递减.
(2)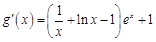 ,由(1)易知,当
,由(1)易知,当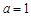 时,
时,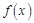 在
在 上的最小值:
上的最小值: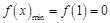
即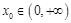 时,
时,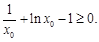 又
又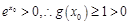 ,
,
曲线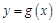 在点
在点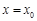 处的切线与
处的切线与 轴垂直等价于方程
轴垂直等价于方程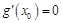 有实数解.
有实数解.
而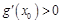 ,即方程
,即方程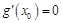 无实数解,故不存在.
无实数解,故不存在.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案
相关题目
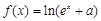 (
( 为常数)是实数集
为常数)是实数集 上的奇函数,函数
上的奇函数,函数 是区间[-1,1]上的减函数.
是区间[-1,1]上的减函数. 在
在 及
及 所在的取值范围上恒成立,求
所在的取值范围上恒成立,求 的取值范围;
的取值范围; 的方程
的方程 的根的个数.
的根的个数. 满足
满足 且
且 .
. 时,不等式:
时,不等式: 恒成立,求实数
恒成立,求实数 的范围.
的范围.
 ,求
,求 的最大值;
的最大值;  ,离心率为
,离心率为 ,且过点
,且过点 ,
,
 (其中
(其中 为参数)所过的定点
为参数)所过的定点 恰在双曲线上,求证:
恰在双曲线上,求证: 。
。 ,直线
,直线 与椭圆C交于不同的两点M,N,以线段MN为直径作圆P。
与椭圆C交于不同的两点M,N,以线段MN为直径作圆P。 直线
直线 ,且直线
,且直线 与曲线
与曲线 相切于点
相切于点 ,求直线
,求直线 的坐标。
的坐标。