题目内容

若a⊥平面α，b与a所成角的余弦为
3
4
，则b与平面α所成角的正弦为（　　）
分析：将直线a平移至a'，使a'与b相交与点A，交平面α于点B，设直线b与平面α交于点C，连接BC，根据异面直线所成角的定义可知∠CAB为b与a所成角，从而cos∠CAB=
3
4
=
AB
AC
，根据线面所成角的定义可知∠ACB为b与平面α所成角，在直角三角形ABC中求出所求．
解答：解：将直线a平移至a'，使a'与b相交与点A，交平面α于点B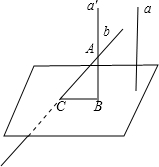
设直线b与平面α交于点C，连接BC
∴∠CAB为b与a所成角，则cos∠CAB=
3
4
=
AB
AC
，
∵a⊥平面α，a∥a'
∴a'⊥平面α
∴∠ACB为b与平面α所成角，sin∠ACB=
AB
AC
=
3
4

故选B．
点评：本题主要考查了异面直线所成角，以及线面所成角，同时考查了作图能力，属于中档题．
练习册系列答案
相关题目
有下列几个命题：①若
a
与
b
-
c
都是非零向量，则“
a
•
b
=
a
•
c
”是“
a
⊥(
b
-
c
)”的充要条件；②已知等腰△ABC的腰为底的2倍，则顶角A的正切值是
15
7
；③在平面直角坐标系xoy中，四边形ABCD的边AB∥DC，AD∥BC，已知点A（-2，0），B（6，8），C（8，6），则D点的坐标为（0，-1）；④设
a
，
b
，
c
为同一平面内具有相同起点的任意三个非零向量，且满足
a
与
b
不共线，
a
⊥
c
，|
a
|=|
c
|，则|
b
•
c
|的值一定等于以
a
，
b
为邻边的平行四边形的面积．其中正确命题的序号是
 
．（写出全部正确结论的序号）

若直线a∥直线b，且a∥平面，则b与a的位置关系是（  ）

A、一定平行      B、不平行

C、平行或相交    D、平行或在平面内

 
有下列几个命题：①若
a
与
b
-
c
都是非零向量，则“
a
•
b
=
a
•
c
”是“
a
⊥(
b
-
c
)”的充要条件；②已知等腰△ABC的腰为底的2倍，则顶角A的正切值是
15
7
；③在平面直角坐标系xoy中，四边形ABCD的边AB∥DC，AD∥BC，已知点A（-2，0），B（6，8），C（8，6），则D点的坐标为（0，-1）；④设
a
，
b
，
c
为同一平面内具有相同起点的任意三个非零向量，且满足
a
与
b
不共线，
a
⊥
c
，|
a
|=|
c
|，则|
b
•
c
|的值一定等于以
a
，
b
为邻边的平行四边形的面积．其中正确命题的序号是______．（写出全部正确结论的序号）
已知a，b，c为三条不同的直线，且a?平面M，b?平面N，M∩N=c，则下面四个命题中正确的是（ ）
A．若a与b是平行两直线，则c至少与a，b中的一条相交
B．若a⊥b，a⊥c，则必有M⊥N
C．若a不垂直于c，则a与b一定不垂直
D．若a∥b，则a∥c
已知a，b，c为三条不同的直线，且a?平面M，b?平面N，M∩N=c，则下面四个命题中正确的是（ ）
A．若a与b是平行两直线，则c至少与a，b中的一条相交
B．若a⊥b，a⊥c，则必有M⊥N
C．若a不垂直于c，则a与b一定不垂直
D．若a∥b，则a∥c

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网