Question

在矩形ABCD中，AB=1，BC=，PA⊥面ABCD，PA=1，则PC与面ABCD所成的角是

1. A.
   30°
2. B.
   45°
3. C.
   60°
4. D.
   90°

Answer 1

A
分析：连接AC，由PA⊥面ABCD，可得∠PAC是PC与面ABCD所成的角，即为所求角，再结合题中条件与三角形的有关知识即可得到答案．
解答：连接AC，如图所示：

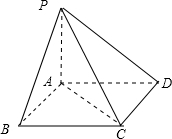
因为PA⊥面ABCD，
所以∠PAC是PC与面ABCD所成的角，即为所求角．
因为在矩形ABCD中，AB=1，BC=，
所以AC=，
又因为PA=1，
所以tan∠PAC=，
所以PC与面ABCD所成的角∠PAC是30°．
故选A．
点评：此题主要考查线面角，空间角解决的关键是做角，由图形的结构及题设条件正确作出平面角来，是求角的关键，也可以根据几何体的结构特征建立空间直角坐标系利用向量的有关知识解决空间角等问题．