题目内容
不共面的四个定点到平面α的距离都相等,这样的平面α共有
7
7
个.分析:根据不共面的四个定点构造出三棱锥,再根据平面两侧的点的个数进行分类,利用三棱锥的结构特征进行求解即可.
解答: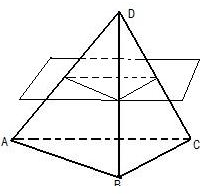 解:空间中不共面的四个定点构成三棱锥,如图:三棱锥D-ABC,
解:空间中不共面的四个定点构成三棱锥,如图:三棱锥D-ABC,
平面α到三棱锥D-ABC的四个定点距离相等,分成两类:
一类是:当平面一侧有一点,另一侧有三点时,即对此三棱锥进行换低,则三棱锥由四种表示形式,
此时满足条件的平面个数是四个,
另一类是:当平面一侧有两点,另一侧有两点时,即构成的直线是三棱锥的相对棱,因三棱锥的相对棱有三对,
则此时满足条件的平面个数是三个,
综上所述,满足条件的平面共有7个,
故答案为:7.
 解:空间中不共面的四个定点构成三棱锥,如图:三棱锥D-ABC,
解:空间中不共面的四个定点构成三棱锥,如图:三棱锥D-ABC,平面α到三棱锥D-ABC的四个定点距离相等,分成两类:
一类是:当平面一侧有一点,另一侧有三点时,即对此三棱锥进行换低,则三棱锥由四种表示形式,
此时满足条件的平面个数是四个,
另一类是:当平面一侧有两点,另一侧有两点时,即构成的直线是三棱锥的相对棱,因三棱锥的相对棱有三对,
则此时满足条件的平面个数是三个,
综上所述,满足条件的平面共有7个,
故答案为:7.
点评:本小题主要考查平面的基本性质及推论、三棱锥的结构特征等基础知识,考查空间想象能力.属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 的距离都相等,这样的平面
的距离都相等,这样的平面 个 B
个 B  个 C
个 C  个 D
个 D  个
个