题目内容
11、不共面的四个定点到平面α的距离都相等,这样的平面α共有( )
分析:根据题意画出构成的几何体,根据平面两侧的点的个数进行分类,利用三棱锥的结构特征进行求解.
解答: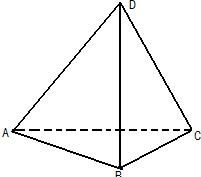 解:空间中不共面的四个定点构成三棱锥,如图:三棱锥D-ABC,
解:空间中不共面的四个定点构成三棱锥,如图:三棱锥D-ABC,
①当平面一侧有一点,另一侧有三点时,即对此三棱锥进行换低,则三棱锥由四种表示形式,此时满足条件的平面个数是四个,
②当平面一侧有两点,另一侧有两点时,即构成的直线是三棱锥的相对棱,因三棱锥的相对棱有三对,则此时满足条件的平面个数是三个,
所以满足条件的平面共有7个,
故选D.
 解:空间中不共面的四个定点构成三棱锥,如图:三棱锥D-ABC,
解:空间中不共面的四个定点构成三棱锥,如图:三棱锥D-ABC,①当平面一侧有一点,另一侧有三点时,即对此三棱锥进行换低,则三棱锥由四种表示形式,此时满足条件的平面个数是四个,
②当平面一侧有两点,另一侧有两点时,即构成的直线是三棱锥的相对棱,因三棱锥的相对棱有三对,则此时满足条件的平面个数是三个,
所以满足条件的平面共有7个,
故选D.
点评:本题考查了三棱锥的结构特征的应用,根据题意画出对应的几何体,再由题意和结构特征进行求解,考查了空间想象能力.

练习册系列答案
相关题目
 的距离都相等,这样的平面
的距离都相等,这样的平面 个 B
个 B  个 C
个 C  个 D
个 D  个
个