题目内容
六张卡片上分别写有数字1,1,2,3,4,5,从中取四张排成一排,可以组成不同的四位奇数的个数为( )
| A.180 | B.126 | C.93 | D.60 |
B
解析试题分析:若四位奇数的个位数为1时有 个,若个位数为3且没有1时有
个,若个位数为3且没有1时有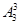 个,若个位数3且仅有一个1时有
个,若个位数3且仅有一个1时有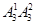 个,若个位数为3且有两个1时有
个,若个位数为3且有两个1时有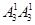 个,即个位数为3时共有
个,即个位数为3时共有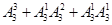 个,同理若个位数为5时亦有
个,同理若个位数为5时亦有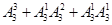 ,所以所求四位奇数的个数为
,所以所求四位奇数的个数为 .正确答案为B.
.正确答案为B.
考点:排列与组合

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知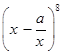 展开式中常数项为5670,其中
展开式中常数项为5670,其中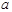 是常数,则展开式中各项系数的和是( )
是常数,则展开式中各项系数的和是( )
| A.28 | B.48 | C.28或48 | D.1或28 |
若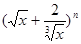 展开式中存在常数项,则n的值可以是( )
展开式中存在常数项,则n的值可以是( )
A.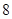 | B.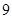 | C.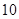 | D.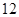 |
若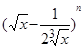 的展开式中第四项为常数项,则
的展开式中第四项为常数项,则 ( )
( )
A. | B.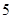 | C. | D.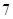 |
用0,1,…,9十个数字,可以组成有重复数字的三位数的个数为( )
| A.243 | B.252 | C.261 | D.279 |
若 展开式中只有第六项的二项式系数最大,则展开式中的常数项是( )
展开式中只有第六项的二项式系数最大,则展开式中的常数项是( )
A. | B.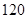 | C.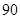 | D.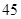 |
若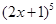 =
=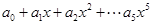 ,则
,则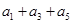 的值为( )
的值为( )
| A.121 | B.124 | C.122 | D.120 |
现需编制一个八位的序号,规定如下:①序号由4个数字和2个x、1个y、1个z组成;②2个x不能连续出现,且y在z的前面;③数字在0、1、2、…、9之间任选,可重复,且四个数字之积为8.则符合条件的不同的序号种数有( )
| A.12600 | B.6300 | C.5040 | D.2520 |
将字母a,a,b,b,c,c排成三行两列,要求每行的字母互不相同,每列的字母也互不相同,则不同的排列方法共有( )
| A.12种 | B.18种 | C.24种 | D.36种 |