题目内容
设a>1,且 ,则
,则 的大小关系为( )
的大小关系为( )
| A.n>m>p | B.m>p>n | C.m>n>p | D.p>m>n |
B
解析试题分析:∵a>1,∴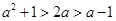 ,又函数
,又函数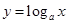 为增函数,故
为增函数,故 ,即m>p>n,故选B
,即m>p>n,故选B
考点:本题考查了对数的性质
点评:熟练运用对数函数的单调性比较大小是解决此类问题的关键,属基础题

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目
已知函数 ,对任意实数x都有
,对任意实数x都有 成立,若当
成立,若当 时,
时, 恒成立,则b的取值范围是( )
恒成立,则b的取值范围是( )
A. | B. | C. 或 或 | D.不能确定 |
已知 ,则
,则 的值为( )
的值为( )
A. | B. | C.1 | D.2 |
函数 的单调递增区间为( )
的单调递增区间为( )
A. | B. | C. | D. |
对数式 有意义,则实数
有意义,则实数 的取值范围是
的取值范围是
| A.(3,4)∪(4,7) | B.(3,7) | C.(-∞,7) | D.(3,+∞) |
设函数 ,且
,且 恒成立,则对
恒成立,则对 ,下面不等式恒成立的是( )
,下面不等式恒成立的是( )
A. | B. | C. | D. |
设 则
则 的值为( )
的值为( )
A. | B. | C. | D. |
已知函数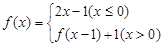 ,把函数
,把函数 的零点按从小到大的顺序排列成一个数列,该数列的前
的零点按从小到大的顺序排列成一个数列,该数列的前 项的和
项的和 ,则
,则 = ( )
= ( )
| A.45 | B.55 | C. | D. |
已知函数 ,若
,若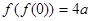 ,则实数
,则实数 等于( )
等于( )
A.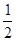 | B. | C.9 | D.2 |