题目内容
（2012•威海二模）如图，菱形ABCD的边长为2，∠A=60°，M为DC的中点，若N为菱形内任意一点（含边界），则| AM |
| AN |
分析：先以点A位坐标原点建立的直角坐标系，求出其它各点的坐标，然后利用点的坐标表示出
•
，把所求问题转化为在平面区域内求线性目标函数的最值问题求解即可．
| AM |
| AN |
解答：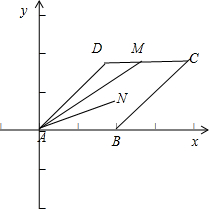
解：：以点A位坐标原点建立如图所示的直角坐标系，由于菱形ABCD的边长为2，∠A=60°，M为DC的中点，
故点A（0，0），则B（2，0），C（3，
），D（1，
），M（2，
）．
设N（x，y），N为平行四边形内（包括边界）一动点，对应的平面区域即为平行四边形ABCD及其内部区域．
因为
=（2，
），
=（x，y），则
•
=2x+
y，
结合图象可得当目标函数z=2x+
y 过点C（3，
）时，z=2x+
y取得最大值为9，
故选D．
解：：以点A位坐标原点建立如图所示的直角坐标系，由于菱形ABCD的边长为2，∠A=60°，M为DC的中点，故点A（0，0），则B（2，0），C（3，
| 3 |
| 3 |
| 3 |
设N（x，y），N为平行四边形内（包括边界）一动点，对应的平面区域即为平行四边形ABCD及其内部区域．
因为
| AM |
| 3 |
| AN |
| AM |
| AN |
| 3 |
结合图象可得当目标函数z=2x+
| 3 |
| 3 |
| 3 |
故选D．
点评：本题主要考查向量在几何中的应用以及数形结合思想的应用和转化思想的应用，是对基础知识和基本思想的考查，属于中档题．
练习册系列答案
相关题目
（2012•威海二模）如图，边长为2的正方形内有一不规则阴影部分，随机向正方形内投入200粒芝麻，恰有60粒落入阴影部分，则不规则图形的面积为（ ）
（2012•威海二模）某商场调查旅游鞋的销售情况，随机抽取了部分顾客的购鞋尺寸，整理得如下频率分布直方图，其中直方图从左至右的前3个小矩形的面积之比为1：2：3，则购鞋尺寸在[39.5，43.5）内的顾客所占百分比为