题目内容

有穷数列{an}，Sn为其前n项和，定义Tn=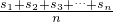数学公式为数列{an}的“凯森和”，如果有99项的数列a1、a2、a3、…、a99的“凯森和”为1000，则有100项的数列1、a1、a2、a3、…、a99的“凯森和”T100=________

991
分析：由题意可知S1+S2+S3+…+Sn=na1+（n-1）a2+（n-2）a3+…+2an-1+an，由此入手，能够求出数列1、a1、a2、a3、…、a99的“凯森和”，即得答案．
解答：∵S1=a1，Sn=a1+a2+…+an，
∴S1+S2+S3+…+Sn=na1+（n-1）a2+（n-2）a3+…+2an-1+an，
对于数列a1，a2，…，a99
∴S1+S2+S3+…+S99=99a1+98a2+97a3+…+2a98+a99=1000n=99000，
对于数列1，a1，a2，…，a100
S1+S2+S3+…+S100=100+99a1+98a2+97a3+…+2a98+a99=99100；
所以数列1、a1、a2、a3、…、a99的“凯森和”T100=991．
点评：本题考查数列的性质和应用，解题时要认真审题．仔细求解，避免出错．
练习册系列答案
相关题目
21、对于每项均是正整数的数列A：a1，a2，…，an，定义变换T1，T1将数列A变换成数列T1（A）：n，a1-1，a2-1，…，an-1．
对于每项均是非负整数的数列B：b1，b2，…，bm，定义变换T2，T2将数列B各项从大到小排列，然后去掉所有为零的项，得到数列T2（B）；
又定义S（B）=2（b1+2b2+…+mbm）+b12+b22+…+bm2．设A0是每项均为正整数的有穷数列，令Ak+1=T2（T1（Ak））（k=0，1，2，…）．
（Ⅰ）如果数列A0为5，3，2，写出数列A1，A2；
（Ⅱ）对于每项均是正整数的有穷数列A，证明S（T1（A））=S（A）；
（Ⅲ）证明：对于任意给定的每项均为正整数的有穷数列A0，存在正整数K，当k≥K时，S（Ak+1）=S（Ak）．
若有穷数列{an} 满足条件a1=an，a2=an-1，…，an=a1，即ai=an-i+1（i=1，2，…，n），则称数列{an} 为“对称数列”．例如，数列1，2，3，2，1与数列4，2，1，1，2，4都是“对称数列”．
（Ⅰ）设{bn}是21项的“对称数列”，其中b1，b2，…，b11是等比数列，且b2=2，b5=16，求{bn}的所有项的和S；
（Ⅱ）设{cn}是22项的“对称数列”，其中c12，c13，…，c22是首项为22，公差为-2的等差数列，求{cn}的前n项和Tn（1≤n≤22，n∈N*）．

若有穷数列{an} 满足条件a1=an，a2=an-1，…，an=a1，即ai=an-i+1（i=1，2，…，n），则称数列{an} 为“对称数列”．例如，数列1，2，3，2，1与数列4，2，1，1，2，4都是“对称数列”．
（Ⅰ）设{bn}是21项的“对称数列”，其中b1，b2，…，b11是等比数列，且b2=2，b5=16，求{bn}的所有项的和S；
（Ⅱ）设{cn}是22项的“对称数列”，其中c12，c13，…，c22是首项为22，公差为-2的等差数列，求{cn}的前n项和Tn（1≤n≤22，n∈N*）．
若有穷数列{an} 满足条件a1=an，a2=an-1，…，an=a1，即ai=an-i+1（i=1，2，…，n），则称数列{an} 为“对称数列”．例如，数列1，2，3，2，1与数列4，2，1，1，2，4都是“对称数列”．
（Ⅰ）设{bn}是21项的“对称数列”，其中b1，b2，…，b11是等比数列，且b2=2，b5=16，求{bn}的所有项的和S；
（Ⅱ）设{cn}是22项的“对称数列”，其中c12，c13，…，c22是首项为22，公差为-2的等差数列，求{cn}的前n项和Tn（1≤n≤22，n∈N*）．
若有穷数列{an} 满足条件a1=an，a2=an-1，…，an=a1，即ai=an-i+1（i=1，2，…，n），则称数列{an} 为“对称数列”．例如，数列1，2，3，2，1与数列4，2，1，1，2，4都是“对称数列”．
（Ⅰ）设{bn}是21项的“对称数列”，其中b1，b2，…，b11是等比数列，且b2=2，b5=16，求{bn}的所有项的和S；
（Ⅱ）设{cn}是22项的“对称数列”，其中c12，c13，…，c22是首项为22，公差为-2的等差数列，求{cn}的前n项和Tn（1≤n≤22，n∈N*）．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网