题目内容
若有穷数列{an} 满足条件a1=an,a2=an-1,…,an=a1,即ai=an-i+1(i=1,2,…,n),则称数列{an} 为“对称数列”.例如,数列1,2,3,2,1与数列4,2,1,1,2,4都是“对称数列”.(Ⅰ)设{bn}是21项的“对称数列”,其中b1,b2,…,b11是等比数列,且b2=2,b5=16,求{bn}的所有项的和S;
(Ⅱ)设{cn}是22项的“对称数列”,其中c12,c13,…,c22是首项为22,公差为-2的等差数列,求{cn}的前n项和Tn(1≤n≤22,n∈N*).
分析:(I)求出前11项构成的等比数列的公比,利用等比数列的前n项和公式求出前11项的和乘以2再减去第11项即得到{bn}的所有项的和S.
(II)对n分段讨论,当1≤n≤11时以22为第11项,公差为2的等差数列,利用等差数列的前n项和求出{cn}的前n项和Tn,当12≤n≤22时,利用等差数列的前n项和求出前11项的和再加上以首项为22,公差为-2前n-11项的和
(II)对n分段讨论,当1≤n≤11时以22为第11项,公差为2的等差数列,利用等差数列的前n项和求出{cn}的前n项和Tn,当12≤n≤22时,利用等差数列的前n项和求出前11项的和再加上以首项为22,公差为-2前n-11项的和
解答:解:(Ⅰ)设数列bn的公比为q,则b5=b2q3=2q3=16,解得q=2,
S=b1+b2+..+b21=2(b1+b2++b11)-b11=2(1+2+22++210)-210=2(211-1)-210=3070.(6分)
(Ⅱ)∵数列cn是“对称数列”,其中c12,c13,,c22是首项为22,公差为-2的等差数列,
∴c22=22-2×10=2,∴c1,c2,,c11是首项为2,公差为2的等差数列.
当1≤n≤11时,Tn=c1+c2+…+cn=2n+
•2=n2+n,
当12≤n≤22时,Tn=c1+c2+..+cn=T11+(c12+c13++cn)=132+22•(n-11)+
×(-2)=-n2+45n-242,
综上所述,Tn=
(13分)
S=b1+b2+..+b21=2(b1+b2++b11)-b11=2(1+2+22++210)-210=2(211-1)-210=3070.(6分)
(Ⅱ)∵数列cn是“对称数列”,其中c12,c13,,c22是首项为22,公差为-2的等差数列,
∴c22=22-2×10=2,∴c1,c2,,c11是首项为2,公差为2的等差数列.
当1≤n≤11时,Tn=c1+c2+…+cn=2n+
| n(n-1) |
| 2 |
当12≤n≤22时,Tn=c1+c2+..+cn=T11+(c12+c13++cn)=132+22•(n-11)+
| (n-11)(n-12) |
| 2 |
综上所述,Tn=
|
点评:求数列的前n项和关键是求出数列的通项,据数列通项的特点选择合适的求和方法.

练习册系列答案
相关题目
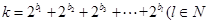 ,且
,且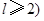 ,求m的最小值.
,求m的最小值.