题目内容
已知函数g(x)=ax2-2ax+1+b(a≠0,b<1),在区间[2,3]上有最大值4,最小值1,设f(x)=| g(x) |
| x |
(Ⅰ)求a,b的值;
(Ⅱ)不等式f(2x)-k•2x≥0在x∈[-1,1]上恒成立,求实数k的范围;
(Ⅲ)方程f(|2x-1|)+k(
| 2 |
| |2x-1| |
分析:(Ⅰ)只需要利用好所给的在区间[2,3]上有最大值4,最小值1,即可列出方程求的两个未知数;
(Ⅱ)要结合(Ⅰ)的结论将问题具体化,在通过游离参数化为求函数?(t)=t2-2t+1最小值问题即可获得问题的解答;
(Ⅲ)可直接对方程进行化简、换元结合函数图象即可获得问题的解答.
(Ⅱ)要结合(Ⅰ)的结论将问题具体化,在通过游离参数化为求函数?(t)=t2-2t+1最小值问题即可获得问题的解答;
(Ⅲ)可直接对方程进行化简、换元结合函数图象即可获得问题的解答.
解答: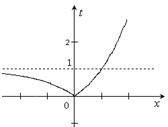 解:(Ⅰ)(1)g(x)=a(x-1)2+1+b-a
解:(Ⅰ)(1)g(x)=a(x-1)2+1+b-a
当a>0时,g(x)在[2,3]上为增函数
故
?
?
当a<0时,g(x)在[2,3]上为减函数
故
?
?
∵b<1
∴a=1,b=0
(Ⅱ)由(Ⅰ)即g(x)=x2-2x+1.f(x)=x+
-2.
方程f(2x)-k•2x≥0化为2x+
-2≥k•2x
1+(
)2-2
≥k,
令
=t,k≤t2-2t+1
∵x∈[-1,1]∴t∈[
,2]记?(t)=t2-2t+1
∴φ(t)min=0
∴k≤0
(Ⅲ)方程f(|2x-1|)+k(
-3)=0
化为|2x-1|+
-(2+3k)=0
|2x-1|2-(2+3k)|2x-1|+(1+2k)=0,|2x-1|≠0
令|2x-1|=t,则方程化为t2-(2+3k)t+(1+2k)=0(t≠0)
∵方程|2x-1|+
-(2+3k)=0有三个不同的实数解,
∴由t=|2x-1|的图象知,
t2-(2+3k)t+(1+2k)=0有两个根t1、t2,
且0<t1<1<t2或0<t1<1,t2=1
记?(t)=t2-(2+3k)t+(1+2k)
则
或
∴k>0.
 解:(Ⅰ)(1)g(x)=a(x-1)2+1+b-a
解:(Ⅰ)(1)g(x)=a(x-1)2+1+b-a当a>0时,g(x)在[2,3]上为增函数
故
|
|
|
当a<0时,g(x)在[2,3]上为减函数
故
|
|
|
∵b<1
∴a=1,b=0
(Ⅱ)由(Ⅰ)即g(x)=x2-2x+1.f(x)=x+
| 1 |
| x |
方程f(2x)-k•2x≥0化为2x+
| 1 |
| 2x |
1+(
| 1 |
| 2x |
| 1 |
| 2x |
令
| 1 |
| 2x |
∵x∈[-1,1]∴t∈[
| 1 |
| 2 |
∴φ(t)min=0
∴k≤0
(Ⅲ)方程f(|2x-1|)+k(
| 2 |
| |2x-1| |
化为|2x-1|+
| 1+2k |
| |2x-1| |
|2x-1|2-(2+3k)|2x-1|+(1+2k)=0,|2x-1|≠0
令|2x-1|=t,则方程化为t2-(2+3k)t+(1+2k)=0(t≠0)
∵方程|2x-1|+
| 1+2k |
| |2x-1| |
∴由t=|2x-1|的图象知,
t2-(2+3k)t+(1+2k)=0有两个根t1、t2,
且0<t1<1<t2或0<t1<1,t2=1
记?(t)=t2-(2+3k)t+(1+2k)
则
|
|
∴k>0.
点评:本题考查的是函数与方程以、恒成立问题以及解的个数的综合类问题.在解答的过程当中充分体现了函数与方程的思想、恒成立的思想以及数形结合和问题转化的思想.值得同学们体会反思.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目