题目内容
6.已知x的对数,求x:(1)lgx=1ga+lgb;
(2)logax=logam-logan;
(3)lgx=31gn-lgm;
(4)logax=$\frac{1}{2}$logab-logac.
分析 (1)(2)(3)(4)利用对数的运算法则即可得出.
解答 解:(1)∵lgx=1ga+lgb=lg(ab),∴x=ab;
(2)logax=logam-logan=$lo{g}_{a}\frac{m}{n}$,∴x=$\frac{m}{n}$;
(3)lgx=31gn-lgm=$lg\frac{{n}^{3}}{m}$,∴$x=\frac{{n}^{3}}{m}$;
(4)logax=$\frac{1}{2}$logab-logac=$lo{g}_{a}\frac{\sqrt{b}}{c}$,∴x=$\frac{\sqrt{b}}{c}$.
点评 本题考查了对数的运算性质、方程的解法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
14.设P为不等式组$\left\{\begin{array}{l}{(2+\sqrt{3})x-y-1≥0}\\{x+y-1≤0}\\{y≥0}\end{array}\right.$所表示的区域内任意一点,过P作圆(x-2)2+(y-1)2=1的切线,切点为A,B,则∠APB的取值范围是( )
| A. | [$\frac{π}{6}$,$\frac{π}{3}$] | B. | [$\frac{π}{6}$,$\frac{π}{4}$] | C. | [$\frac{π}{4}$,$\frac{π}{2}$] | D. | [$\frac{π}{3}$,$\frac{π}{2}$] |
18.已知集合A={x|y=$\sqrt{3x-{x}^{2}}$},B={x|$\frac{x+1}{x-2}$<0},则A∩B=( )
| A. | {x|0<x<2} | B. | {x|0≤x<2} | C. | {x|-1<x≤3} | D. | {x|2<x≤3} |
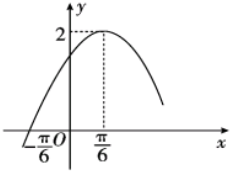 函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,0<φ<$\frac{π}{2}$)的部分图象如图所示.
函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,0<φ<$\frac{π}{2}$)的部分图象如图所示.