题目内容
设a、b∈R+,a≠b,x,y∈(0,+∞),则 ,当且仅当
,当且仅当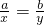 时,上式取等号,利用以上结论,可以得到函数
时,上式取等号,利用以上结论,可以得到函数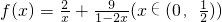 的最小值为
的最小值为
- A.169
- B.121
- C.25
- D.16
C
分析:可得原式= ≥
≥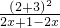 =25,验证等号成立的条件即可.
=25,验证等号成立的条件即可.
解答:由题意可得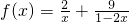 =
=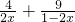
= ≥
≥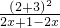 =25
=25
当且仅当 ,即x=
,即x= 时,取等号.
时,取等号.
故函数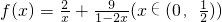 的最小值为25
的最小值为25
故选C
点评:本题考查基本不等式求最值,利用已知构造可利用的式子是解决问题的关键,属基础题.
分析:可得原式=
 ≥
≥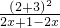 =25,验证等号成立的条件即可.
=25,验证等号成立的条件即可.解答:由题意可得
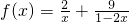 =
=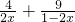
=
 ≥
≥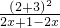 =25
=25当且仅当
 ,即x=
,即x= 时,取等号.
时,取等号.故函数
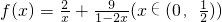 的最小值为25
的最小值为25故选C
点评:本题考查基本不等式求最值,利用已知构造可利用的式子是解决问题的关键,属基础题.

练习册系列答案
相关题目