题目内容
(1)(用综合法证明) 若a>0,b>0,求证:(a+b)(| 1 |
| a |
| 1 |
| b |
(2)(用反证法证明) 已知x,y∈R+,且x+y>2,求证:
| 1+x |
| y |
| 1+y |
| x |
分析:(1)根据a>0,b>0,可得a+b≥2
,同理可证
+
≥2
,相乘即得所证.
(2)假设
与
都大于或等于2,可得
,从而推出x+y≤2,这与x+y>2矛盾,故假设不成立,
命题得证.
| ab |
| 1 |
| a |
| 1 |
| b |
|
(2)假设
| 1+x |
| y |
| 1+y |
| x |
|
命题得证.
解答:解:(1)证明:∵a>0,b>0,
∴a+b≥2
,(当且仅当a=b时,取“=”号)…(2分)
∴
+
≥2
,∴(a+b)(
+
)≥4. …(6分)
(2)假设:
与
都大于或等于2,
∵x,y∈R*,∴
,
∴2+x+y≥2x+2y,∴x+y≤2,这与x+y>2矛盾,…(11分)
∴假设不成立.
所以,
与
中至少有一个小于2. …(12分)
∴a+b≥2
| ab |
∴
| 1 |
| a |
| 1 |
| b |
|
| 1 |
| a |
| 1 |
| b |
(2)假设:
| 1+x |
| y |
| 1+y |
| x |
∵x,y∈R*,∴
|
∴2+x+y≥2x+2y,∴x+y≤2,这与x+y>2矛盾,…(11分)
∴假设不成立.
所以,
| 1+x |
| y |
| 1+y |
| x |
点评:本题考查用综合法法和反证法证明不等式,用反证法证明数学命题时,推出矛盾,是解题的关键和难点,属于中档题.

练习册系列答案
相关题目
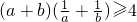
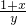 与
与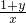 中至少有一个小于2.
中至少有一个小于2.