Question

在面积为1的△PMN中，tan∠PMN=

1

2

，tan∠MNP=-2．建立适当的坐标系，求以M，N为焦点且过点P的椭圆方程．

Answer 1

分析：以MN所在直线为x轴，MN的垂直平分线为y轴建立直角坐标系，设以M，N为焦点且过点P的椭圆方程和焦点坐标，根据tanM=

1

2

，tanα=tg（π-∠MNP）=2，得直线PM和PN的直线方程，将此二方程联立解得x和y，可知点P的坐标，根据，|MN|=2c，MN上的高为点P的纵坐标，根据三角形面积公式表示出出△MNP的面积求得c，则点P的坐标可得．由两点间的距离公式求得|PM|和|PN|，进而根据椭圆的定义求得a，进而求得b，则椭圆方程可得．

解答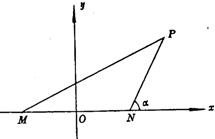：解：如图，以MN所在直线为x轴，MN的垂直平分线为y轴建立直角坐标系，
设以M，N为焦点且过点P的椭圆方程为

x2

a2

+

y2

b2

=1，
焦点为M（-c，0），N（c，0）．
由tan∠MNP=

1

2

，tan∠MNP=-2，tanα=tan（π-∠MNP）=2，
得直线PM和直线PN的方程分别为y=

1

2

（x+c）和y=2（x-c）．
将此二方程联立，解得x=

5

3

c，y=

4

3

c，即P点坐标为（

5

3

c，

4

3

c）．
在△MNP中，|MN|=2c，MN上的高为点P的纵坐标，故S△MNP=

1

2

•2c•

4

3

c=

4

3

c2．
由题设条件S_△MNP=1，∴c=

3

2

，即P点坐标为(

5 3

6

，  

2 3

3

)．
由两点间的距离公式|PM|=

(x+c)2+y2

=

( 5 3 6 + 3 2 )2+( 2 3 3 )2

=

2 15

3

，|PN|=

(x-c)2+y2

=

( 5 3 6 - 3 2 )2+( 2 3 3 )2

=

15

3

．
得a=

1

2

(|PM|+|PN|)=

15

2

．
又b²=a²-c²=

15

4

-

3

4

=3，
故所求椭圆方程为

4x2

15

+

y2

3

=1．

点评：本题主要考查坐标系、椭圆的概念和性质、直线方程以及综合应用能力．