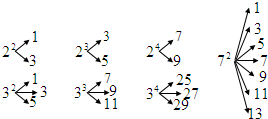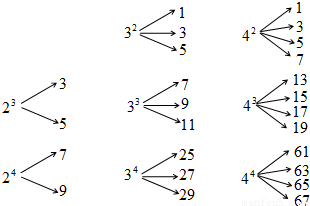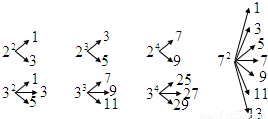题目内容
如图,对大于或等于2的正整数m的n次幂进行如下方式的“分裂”(其中m、n∈N*):例如72的“分裂”中最小的数是1,最大的数是13;若m3的“分裂”中最小的数是211,则m= .
【答案】分析:由题意知,n的三次方就是n 个连续奇数相加,且从2的分裂开始,这些三次方的分解正好是从奇数3开始连续出现,由此规律即可建立m3(m∈N*)的分裂中最小的加数是211的方程,求出m的值即可,
解答:解:由题意,从23到(m-1)3,正好用去从3开始的连续奇数共2+3+4+…+(m-1)=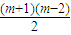 个,
个,
即211=3+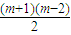 ×2
×2
解得m=15或m=-14(舍去)
故答案为15
点评:本题考查归纳推理,求解的关键是根据归纳推理的原理归纳出结论,如本题是建立关于m的方程的方法,求出m的值.
解答:解:由题意,从23到(m-1)3,正好用去从3开始的连续奇数共2+3+4+…+(m-1)=
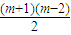 个,
个,即211=3+
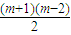 ×2
×2解得m=15或m=-14(舍去)
故答案为15
点评:本题考查归纳推理,求解的关键是根据归纳推理的原理归纳出结论,如本题是建立关于m的方程的方法,求出m的值.

练习册系列答案
 培优三好生系列答案
培优三好生系列答案
相关题目