题目内容
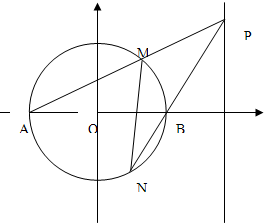 如图:已知A,B是圆x2+y2=4与x轴的交点,P为直线l:x=4上的动点,PA,PB与圆x2+y2=4的另一个交点分别为M,N.
如图:已知A,B是圆x2+y2=4与x轴的交点,P为直线l:x=4上的动点,PA,PB与圆x2+y2=4的另一个交点分别为M,N.
(1)若P点坐标为(4,6),求直线MN的方程;
(2)求证:直线MN过定点.
解:(1)直线PA方程为y=x+2,由  解得M(0,2),…(2分)
解得M(0,2),…(2分)
直线PB的方程 y=3x-6,由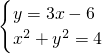 解得 N(
解得 N( ,-
,- ),…(4分)
),…(4分)
用两点式求得MN的方程,并化简可得 y=-2x+2.…(6分)
(2)设P(4,t),则直线PA的方程为 y= (x+2),直线PB的方程为 y=
(x+2),直线PB的方程为 y= (x-2).
(x-2).
由 得 M(
得 M(  ,
, ),同理 N(
),同理 N(  ,
, ). …(10分)
). …(10分)
直线MN的斜率 k= =
= …(12分)
…(12分)
直线MN的方程为 y= (x-
(x- )-
)- ,
,
化简得:y= x-
x- . …(14分)
. …(14分)
所以直线MN过定点(1,0).…(16分)
分析:(1)直线PA方程为y=x+2,由 解得M(0,2),直线PB的方程 y=3x-6,由
解得M(0,2),直线PB的方程 y=3x-6,由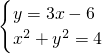 解得 N(
解得 N( ,-
,- ),用两点式求得MN的方程.
),用两点式求得MN的方程.
(2)设P(4,t),则直线PA的方程为 y= (x+2),直线PB的方程为 y=
(x+2),直线PB的方程为 y= (x-2),解方程组求得M、N的坐标,从而得到MN的方程为y=
(x-2),解方程组求得M、N的坐标,从而得到MN的方程为y= x-
x- ,显然过定点(1,0).
,显然过定点(1,0).
点评:本题主要考查直线过定点问题,求直线的方程,求两条直线的交点坐标,属于中档题.
 解得M(0,2),…(2分)
解得M(0,2),…(2分)直线PB的方程 y=3x-6,由
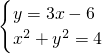 解得 N(
解得 N( ,-
,- ),…(4分)
),…(4分)用两点式求得MN的方程,并化简可得 y=-2x+2.…(6分)
(2)设P(4,t),则直线PA的方程为 y=
 (x+2),直线PB的方程为 y=
(x+2),直线PB的方程为 y= (x-2).
(x-2).由
 得 M(
得 M(  ,
, ),同理 N(
),同理 N(  ,
, ). …(10分)
). …(10分)直线MN的斜率 k=
 =
= …(12分)
…(12分)直线MN的方程为 y=
 (x-
(x- )-
)- ,
,化简得:y=
 x-
x- . …(14分)
. …(14分)所以直线MN过定点(1,0).…(16分)
分析:(1)直线PA方程为y=x+2,由
 解得M(0,2),直线PB的方程 y=3x-6,由
解得M(0,2),直线PB的方程 y=3x-6,由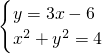 解得 N(
解得 N( ,-
,- ),用两点式求得MN的方程.
),用两点式求得MN的方程.(2)设P(4,t),则直线PA的方程为 y=
 (x+2),直线PB的方程为 y=
(x+2),直线PB的方程为 y= (x-2),解方程组求得M、N的坐标,从而得到MN的方程为y=
(x-2),解方程组求得M、N的坐标,从而得到MN的方程为y= x-
x- ,显然过定点(1,0).
,显然过定点(1,0).点评:本题主要考查直线过定点问题,求直线的方程,求两条直线的交点坐标,属于中档题.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目
 如图,已知A、B是单位圆O上的点,C是圆与x轴正半轴的交点,点A的坐标为
如图,已知A、B是单位圆O上的点,C是圆与x轴正半轴的交点,点A的坐标为 如图:已知A,B是圆x2+y2=4与x轴的交点,P为直线l:x=4上的动点,PA,PB与圆x2+y2=4的另一个交点分别为M,N.
如图:已知A,B是圆x2+y2=4与x轴的交点,P为直线l:x=4上的动点,PA,PB与圆x2+y2=4的另一个交点分别为M,N.
