题目内容
已知向量满足|
|=1，|
|=2，且
在
方向上的投影等于
在
方向上的看投影，则|
-
|=
．
| a |
| b |
| a |
| b |
| b |
| a |
| a |
| b |
| 5 |
| 5 |
分析：根据
在
方向上的投影等于
在
方向上的投影得到两向量垂直，然后把要求的模取平方运算，求出模后开方即可．
| a |
| b |
| b |
| a |
解答：解：设向量
与向量
的夹角为θ，则由题意可知θ=
，
所以|
-
|2=(
-
)2=(
)2-2
•
+(
)2
=|
|2-2|
||
|cos
+|
|2=12+22=5
所以|
-
|=
．
故答案为
．
| a |
| b |
| π |
| 2 |
所以|
| a |
| b |
| a |
| b |
| a |
| a |
| b |
| b |
=|
| a |
| a |
| b |
| π |
| 2 |
| b |
所以|
| a |
| b |
| 5 |
故答案为
| 5 |
点评：本题是向量模长的运算，条件中给出两个向量的模和两向量的夹角，代入数量积的公式运算即可，只是题目所给的向量要应用向量的性质来运算．
练习册系列答案
步步高达标卷系列答案
相关题目
已知向量满足|
|=2|
|，若p：关于x的方程x2+|
|x+
•
=0没有实数根；q：向量
，
的夹角θ∈[0，
），则p是q的（ ）
| a |
| b |
| a |
| a |
| b |
| a |
| b |
| π |
| 6 |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
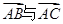满足，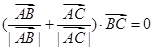
,
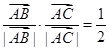，则△ABC为