题目内容

某品牌汽车4店经销三种排量的汽车，其中三种排量的汽车依次有５，4，3款不同车型．某单位计划购买3辆不同车型的汽车，且购买每款车型等可能．
(1)求该单位购买的3辆汽车均为种排量汽车的概率；
(2)记该单位购买的3辆汽车的排量种数为，求的分布列及数学期望．

（1）；（2）详见解析．

解析试题分析：(1)这是一个古典概型问题，先求出从15款车型中任买3辆共有多少种可能，再求出购买3辆车都为B种车有多少种可能，即可求出结果；（2）的所有可能取值为1，2，3，对每种情况要准确分类，求出各种情况下有多少种可能，就可求出各种取值的概率，然后再求数学期望.
试题解析：(1)设该单位购买的3辆汽车均为种排量汽车为事件，则
所以该单位购买的3辆汽车均为种排量汽车的概率为．             4分
(2)随机变量的所有可能取值为1，2，3.
则，
．
所以的分布列为


１
２
３




          8分
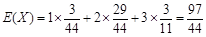数学期望．                 10分
考点：随机变量的概率分布.

练习册系列答案
相关题目

某校高三(1)班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的破坏，可见部分如下：

试根据图表中的信息解答下列问题：
(1)求全班的学生人数及分数在[70,80)之间的频数；
(2)为快速了解学生的答题情况，老师按分层抽样的方法从位于[70,80)，[80,90)和[90,100]分数段的试卷中抽取8份进行分析，再从中任选3人进行交流，求交流的学生中，成绩位于[70,80)分数段的人数X的分布列和数学期望．

盒子中装有四张大小形状均相同的卡片，卡片上分别标有数字－1,0,1,2.称“从盒中随机抽取一张，记下卡片上的数字后并放回”为一次试验(设每次试验的结果互不影响)．
(1)在一次试验中，求卡片上的数字为正数的概率；
(2)在四次试验中，求至少有两次卡片上的数字都为正数的概率；
(3)在两次试验中，记卡片上的数字分别为X，η，试求随机变量X＝X·η的分布列与数学期望E(X)．

已知，，点的坐标为.
（1）求当时，点满足的概率；
（2）求当时，点满足的概率.

设为随机变量，从棱长为1的正方体ABCD-A1B1C1D1的八个顶点中任取四个点，当四点共面时，=0，当四点不共面时，的值为四点组成的四面体的体积．
（1）求概率P（=0）；
（2）求的分布列，并求其数学期望E ()．

为了了解某市工厂开展群众体育活动的情况，拟采用分层抽样的方法从三个区中抽取6个工厂进行调查.已知区中分别有27,18，9个工厂.
（Ⅰ）求从区中应分别抽取的工厂个数；
（Ⅱ）若从抽得的6个工厂中随机地抽取2个进行调查结果的对比，求这2个工厂中至少有1个来自区的概率.

为了调查学生的视力情况，随机抽查了一部分学生的视力，将调查结果分组，分组区间为，经过数据处理，得到如下频率分布表

分组
 		频数
 		频率
 

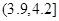 		3
 		0.06
 

 		6
 		0.12
 

 		25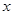
 
 

 
 
 

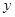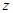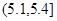 		2
 		0.04
 
合计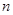
 
 		1.00
 
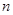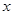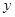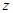（Ⅰ）求频率分布表中未知量，，，的值
（Ⅱ）从样本中视力在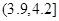和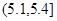的所有同学中随机抽取两人，求两人视力差的绝对值低于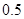的概率

某小组共有、、、、五位同学，他们的身高（单位:米）以及体重指
标（单位:千克/米2）如下表所示：

 





身高





体重指标





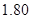（1）从该小组身高低于的同学中任选人，求选到的人身高都在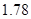以下的概率；
（2）从该小组同学中任选人，求选到的人的身高都在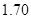以上且体重指标都在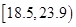中的概率．

某学生参加某高校的自主招生考试，须依次参加A，B，C，D，E五项考试，如果前四项中有两项不合格或第五项不合格，则该考生就被淘汰，考试即结束；考生未被淘汰时，一定继续参加后面的考试．已知每一项测试都是相互独立的，该生参加A，B，C，D四项考试不合格的概率均为，参加第五项不合格的概率为.
(1)求该生被录取的概率；
(2)记该生参加考试的项数为X，求X的分布列和期望．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网