题目内容

若100^a=5，10^b=2，则2a+b=________．

1
分析：先把指数式化为对数式即可得出．
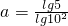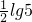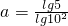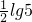解答：∵100^a=5，10^b=2，∴ $\text{[math]}$ = $\text{[math]}$ ，b=lg2，
∴2a+b=lg2+lg5=1．
故答案为1．
点评：把指数式化为对数式是解题的关键．

练习册系列答案

大显身手素质教育单元测评卷系列答案

随堂讲与练系列答案

开放课堂义务教育新课程导学案系列答案

二期课改配套教辅读物系列答案

小学单元测试卷系列答案

新课程单元检测新疆电子音像出版社系列答案

赢在新课堂随堂小测系列答案

品学双优赢在期末系列答案

优等生测评卷系列答案

世纪百通期末金卷系列答案

相关题目

下列结论中正确的个数是（　　）
①当a＜0时，a²＞a³；
②

n	an

=|a|；
③函数y=（x-2）

-（3x-7）⁰的定义域是（2，+∞）；
④若100^a=5，10^b=2，则2a+b=1．

下列结论中正确的是

．（填序号）
①当a＜0时，(a2)

n	an

=|a|；
③函数y=(x-2)

-（3x-7）⁰的定义域是（2，+∞）；
④若100^a=5，10^b=2，则2a+b=1．

若100^a=5，10^b=2，则2a+b=（　　）

若100^a=5，10^b=2，则2a+b=

下列结论中正确的个数是（　　）
①当a＜0时，(a2)

n	an

=|a|；
③函数y=(x-2)

+(3x-7)0的定义域是[2，+∞）；
④若100^a=5，10^b=2，则2a+b=1．