题目内容
(08年周至二中四模理)(12分) 已知函数f(x)=![]() ,记数列{an}的前n项和为Sn,且有a1=f(1),当n≥2时,Sn-
,记数列{an}的前n项和为Sn,且有a1=f(1),当n≥2时,Sn-![]() (n2+5n-2).
(n2+5n-2).
(1)计算a1,a2,a3,a4;
(2)求出数列{an}的通项公式,并给予证明.
解析: (1)由已知,当n≥2时,f(an)=![]() ,
,
∵Sn-![]() , ∴Sn-
, ∴Sn-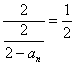 (n2+5n-2),
(n2+5n-2),
即Sn+an=![]() (n2+5n+2). 又a1=f(1)=2,
(n2+5n+2). 又a1=f(1)=2,
由S2+a2=a1+2a2=![]() (22+5×2+2), 得a2=3;
(22+5×2+2), 得a2=3;
由S3+a3=a1+a2+2a3=![]() (32+5×3+2), 解得a3=4;
(32+5×3+2), 解得a3=4;
由S4+a4=a1+a2+a3+2a4=![]() (42+5×4+2) ,解得a4=5. 6分
(42+5×4+2) ,解得a4=5. 6分
(2)则a1=2,a2=3,a3=4,a4=5,于是猜想:an=n+1(n∈N). 8分
以下用数学归纳法证明:
(a)当n=1时命题成立.
(b)设n=k时,ak=k+1(k∈N). 由Sk+1+ak+1=![]() [(k+1)2+5(k+1)+2],
[(k+1)2+5(k+1)+2],
a1+a2+…+ak+2ak+1=![]() (k2+7k+8),
(k2+7k+8),
2ak+1=![]() (k2+7k+8)-(2+3+…+k+1)=
(k2+7k+8)-(2+3+…+k+1)=![]() (k2+7k+8)-
(k2+7k+8)-![]() =
=![]() (k2+7k+8-k2-3k)=2k+4.
(k2+7k+8-k2-3k)=2k+4.
ak+1=(k+1)+1, 即当n=k+1时命题也成立.
故由(a)、(b)知对一切n∈N均有an=n+1.
练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目