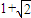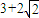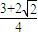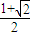题目内容
设直线l:x+y=0,若点A(a,0),B(-2b,4ab)(a>0,b>0)满足条件AB∥l,则
的最小值为( )
| a+b |
A、1+
| ||||
B、3+2
| ||||
C、
| ||||
D、
|
分析:由AB∥l可以找出a和b的关系,4ab=a+2b,故可采用消元法转化为某个变量的函数求最值.
解答:解:由AB∥l得4ab=a+2b,故a=
,因为a>0,b>0,故b>
,
所以a+b=
+b=
+
+b=
+b-
+
≥2
+
=
当且仅当
=b-
即b=
时“=”成立,
故
≥
=
故选D
| 2b |
| 4b-1 |
| 1 |
| 4 |
所以a+b=
| 2b |
| 4b-1 |
| 1 |
| 2 |
| 1 |
| 2(4b-1) |
| 1 |
| 2(4b-1) |
| 1 |
| 4 |
| 3 |
| 4 |
|
| 3 |
| 4 |
3+2
| ||
| 4 |
当且仅当
| 1 |
| 2(4b-1) |
| 1 |
| 4 |
1+
| ||
| 4 |
故
| a+b |
|
1+
| ||
| 2 |
故选D
点评:本题考查直线平行的条件、基本不等式求最值问题,解题中要注意创造性的利用基本不等式.

练习册系列答案
相关题目
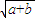 的最小值为( )
的最小值为( )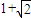
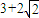

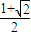
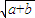 的最小值为( )
的最小值为( )