题目内容
若关于x的方程
（a>0，且
）有解，则m的取值范围是（ ）
A． | B． | C． | D． |
A
解析试题分析：令t=ax（t＞0），则方程转化为在（0，+∞）上有解．
则利用判别式可知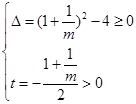
解得参数m的范围是，选A.
考点：本题主要考查了二次方程实根分布问题，同时考查换元转化思想．
点评：解决该试题的关键是由题意可令t=ax（t＞0），则方程转化为二次方程在（0，+∞）上有解，利用实根分布处理即可．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
函数
是（ ）
A．奇函数，且在 上是增函数 | B．奇函数，且在上是减函数 |
| C．偶函数，且在上是增函数 | D．偶函数，且在上是减函数 |
已知二次函数
的导数为
，
，对于任意实数
都有
，则
的最小值为（ ）
| A．3 | B． | C．2 | D． |
已知函数
，若
互不相等，且
，
则
的取值范围是( )
| A．（1，10） | B．（5，6） | C．（10，12） | D．（20，24） |
函数
的值域为（ ）
A． | B． | C． | D． |
函数
的零点的个数为（ ）
| A．0个 | B．1个 | C．2个 | D．3个 |
设f (x)是奇函数，且在（0，＋∞）上是增函数，又f (－3)＝0，则x·f (x)＜0的解集为
| A．{x∣－3＜x＜0或x＞3} |
| B．{x∣x＜－3或0＜x＜3} |
| C．{x∣x＜－3或x＞3} |
| D．{x∣－3＜x＜0或0＜x＜3} |
设
则
的值为( )
| A．6 | B． | C． | D． |
若函数
,若
,则实数
的取值范围是（ ）
| A．（-1，0）∪（0，1） | B．（-∞，-1）∪（1,+∞） |
| C．（-1，0）∪（1,+∞） | D．（-∞，-1）∪（0,1） |