题目内容

已知函数f(x)=2|x-2|+ax(x∈R)有最小值.

(1)求实数a的取值范围.

(2)设g(x)为定义在R上的奇函数,且当x<0时,g(x)=f(x),求g(x)的解析式.

 

(1) [-2,2] (2)

【解析】(1)f(x)=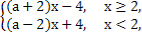

要使函数f(x)有最小值,需∴-2≤a≤2,

即当a∈[-2,2]时,f(x)有最小值.

(2)∵g(x)为定义在R上的奇函数,∴g(0)=0.

设x>0,则-x<0,

∴g(x)=-g(-x)=(a-2)x-4,

∴g(x)=

 

练习册系列答案
相关题目

设函数f(x)＝|x－1|＋|x－2|.

(1)画出函数y＝f(x)的图象；

(2)若不等式|a＋b|＋|a－b|≥|a|f(x)( a≠0，a，b∈R)恒成立，求实数x的取值范围．

 

在平面直角坐标系xOy中，O为坐标原点，A(－2,0)，B(2,0)，点P为动点，且直线AP与直线BP的斜率之积为－.

(1)求动点P的轨迹C的方程；

(2)过点D(1,0)的直线l交轨迹C于不同的两点M，N，△MON的面积是否存在最大值？若存在，求出△MON的面积的最大值及相应的直线方程；若不存在，请说明理由．

 

已知f(x)=则f(f(1))的值等于　　　　.

 

函数f(x)=+lg的定义域是(　　)

(A)(2,4) (B)(3,4)

(C)(2,3)∪(3,4] (D)[2,3)∪(3,4)

 

设函数f(x)=为奇函数,则实数a=　　　　.

 

已知f(x)是周期为2的奇函数,当0<x<1时,f(x)=lgx,设a=f(),b=f(),c=f(),则(　　)

(A)c<a<b (B)a<b<c (C)b<a<c (D)c<b<a

 

已知a=log23.6,b=log43.2,c=log43.6,则(　　)

(A)a>b>c (B)a>c>b

(C)b>a>c (D)c>a>b

 

若不等式x2+ax+1≥0对于一切x∈(0,]恒成立,则a的最小值是(　　)

(A)0 (B)2 (C)- (D)-3

 

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网