题目内容
已知椭圆的两焦点为F1(-| 3 |
| 3 |
| ||
| 2 |
(1)求此椭圆的方程;
(2)设直线l:y=x+m,若l与此椭圆相交于P,Q两点,且|PQ|等于椭圆的短轴长,求m的值.
分析:(1)先设椭圆方程为
+
=1(a>b>0),有c=
,
=
求得a,b,最后写出椭圆方程;
(2)由
,将直线的方程代入抛物线的方程,消去y得到关于x的一元二次方程,再结合根系数的关系利用弦长公式即可求得m值,从而解决问题.
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
| c |
| a |
| ||
| 2 |
(2)由
|
解答:解:(1)设椭圆方程为
+
=1(a>b>0),则c=
,
=
,(4分)
∴a=2,b=1,所求椭圆方程
+y2=1.(5分)
(2)由
,消去y,得5x2+8mx+4(m2-1)=0,
则△>0得m2<5(*)
设P(x1,y1),Q(x2,y2),则x1+x2=-
,x1x2=
y1-y2=x1-x2,(8分)
|PQ|=
=2
解得m=±
,满足(*)
∴m=±
.
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
| c |
| a |
| ||
| 2 |
∴a=2,b=1,所求椭圆方程
| x2 |
| 4 |
(2)由
|
则△>0得m2<5(*)
设P(x1,y1),Q(x2,y2),则x1+x2=-
| 8m |
| 5 |
| 4(m2-1) |
| 5 |
|PQ|=
2[(-
|
解得m=±
| ||
| 4 |
∴m=±
| ||
| 4 |
点评:本题主要考查椭圆的标准方程和几何性质,直线方程,曲线和方程的关系等解析几何的基本思想方法和综合解题能力.解答的关键是利用方程思想利用设而不求的方法求出m值.

练习册系列答案
相关题目
 的左焦点为F,A(-a,0),B(0,b)为椭圆的两个顶点,若F到AB的距离等于
的左焦点为F,A(-a,0),B(0,b)为椭圆的两个顶点,若F到AB的距离等于 ,则椭圆的离心率为( )
,则椭圆的离心率为( )
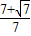


 的右焦点为F(2,0),M为椭圆的上顶点,O为坐标原点,且△MOF是等腰直角三角形.
的右焦点为F(2,0),M为椭圆的上顶点,O为坐标原点,且△MOF是等腰直角三角形. ).
). 的左焦点为F,A(-a,0),B(0,b)为椭圆的两个顶点,若F到AB的距离等于
的左焦点为F,A(-a,0),B(0,b)为椭圆的两个顶点,若F到AB的距离等于 ,则椭圆的离心率为( )
,则椭圆的离心率为( )



 的右焦点为F(2,0),M为椭圆的上顶点,O为坐标原点,且△MOF是等腰直角三角形.
的右焦点为F(2,0),M为椭圆的上顶点,O为坐标原点,且△MOF是等腰直角三角形. ).
). 的左焦点为F,A(-a,0),B(0,b)为椭圆的两个顶点,若F到AB的距离等于
的左焦点为F,A(-a,0),B(0,b)为椭圆的两个顶点,若F到AB的距离等于 ,则椭圆的离心率为( )
,则椭圆的离心率为( )


