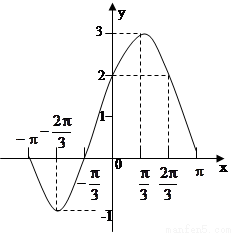题目内容
函数 的部分图象如下图所示,将
的部分图象如下图所示,将 的图象向右平移
的图象向右平移 个单位后得到函数
个单位后得到函数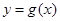 的图象.
的图象.

(1)求函数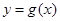 的解析式;
的解析式;
(2) 若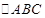 的三边为
的三边为 成单调递增等差数列,且
成单调递增等差数列,且 ,求
,求 的值.
的值.
【答案】
(1)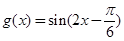 ;(2)
;(2) .
.
【解析】
试题分析:(1)对称中心到相邻对称轴的距离等于四分之和个周期,所以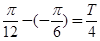 ,由此可得
,由此可得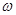 .再将点
.再将点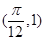 代入
代入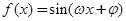 便可求得
便可求得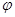 ,这样便得
,这样便得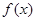 的解析式.再将
的解析式.再将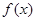 中的
中的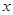 换成
换成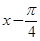 便得
便得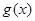 的解析式.
的解析式.
(2)由(1)得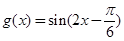 .由
.由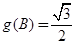 可求出
可求出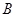 .
.
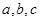 成等差,所以
成等差,所以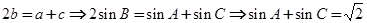 …………①
…………①
如何利用等式①求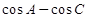 的值?
的值?
注意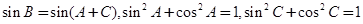 ,所以可令
,所以可令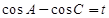 ……②
……②
①②两式平方相加即可.
试题解析:(1)由图知: ,∵
,∵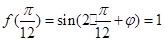 ,
,
∴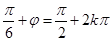 ,即
,即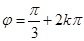 , 由于
, 由于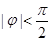 ,所以
,所以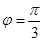 ,
,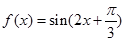 ,函数
,函数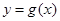 的解析式为
的解析式为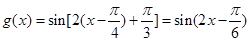 .
.
(2)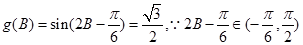 ,且
,且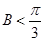 ,所以
,所以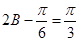 ,
,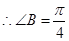 .
.
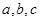 成等差,所以
成等差,所以 ,………………………………①
,………………………………①
令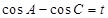 ,………………………………………………………②
,………………………………………………………②
两式平方相加得: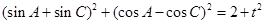 ,
,
整理化简得: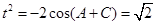 .由于
.由于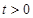 ,所以
,所以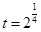 .
.
考点:1、三角函数的图象及其变换;2、正弦定理及三角恒等变换.

练习册系列答案
 名题金卷系列答案
名题金卷系列答案
相关题目
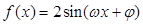
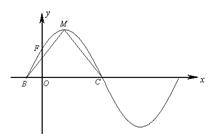
 的部分图象如下图所示,该图象与
的部分图象如下图所示,该图象与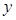 轴交于点
轴交于点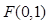 ,与
,与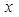 轴交于点
轴交于点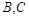 ,
,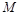 为最高点,且
为最高点,且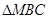 的面积为
的面积为 .
.
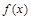 的解析式;
的解析式;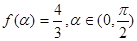 ,求
,求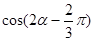 的值.
的值.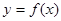 的图象的所有点的横坐标缩短到原来的
的图象的所有点的横坐标缩短到原来的 倍(纵坐标不变),再向左平移
倍(纵坐标不变),再向左平移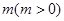 个单位,得函数
个单位,得函数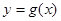 的图象,若函数
的图象,若函数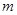 的最小值.
的最小值.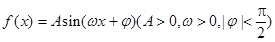 的部分图象如下图所示,则函数
的部分图象如下图所示,则函数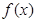 的解析式为
的解析式为 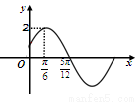
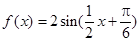 B.
B.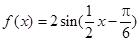
 D.
D.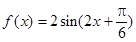
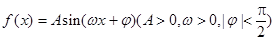 的部分图象如下图所示,则.
的部分图象如下图所示,则.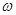 =
=
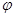 =
= 

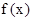 的解析式;
的解析式;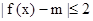 在
在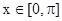 上[来源:Z.xx.k.Com]
上[来源:Z.xx.k.Com]