题目内容
设m为实数,函数![]() ,
,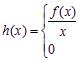
![]() .
.
(1)若![]() ≥4,求m的取值范围;
≥4,求m的取值范围;
(2)当m>0时,求证![]() 在
在![]() 上是单调递增函数;
上是单调递增函数;
(3)若![]() 对于一切
对于一切![]() ,不等式
,不等式![]() ≥1恒成立,求实数m的取值范围.
≥1恒成立,求实数m的取值范围.
(1)![]() (2)见解析 (3)
(2)见解析 (3)![]()
解析:
(1)![]()
当![]() 时,
时,![]() ,无解;
,无解;
当![]() 时,
时,![]() ,解得
,解得![]() 。
。
所以![]() 。
。
(2)由于![]() 。所以
。所以![]() 。
。
任取![]() ,
,![]()
![]()
所以![]()
即:![]() 在
在![]() 为单调递增函数。
为单调递增函数。
(3)、① ![]() 时,
时, ![]() ,
,![]() 恒成立
恒成立![]() 恒成立 ,即:
恒成立 ,即:![]()
由于![]() 的对称轴为
的对称轴为![]()
![]()
故![]() 在
在![]() 为单调递增函数,故
为单调递增函数,故![]() 。
。
所以![]() 。
。
② 当![]() 时,
时,
![]()
易证 ![]() 在
在![]() 为递增,
为递增,
由②得![]() 在
在![]() 为递增,
为递增,
所以,![]() ,即
,即![]() , 所以
, 所以 ![]() 。
。
当![]() 时,
时,![]() (无解)
(无解)
综上所述 ![]() 。
。

练习册系列答案
相关题目
 .
. .
. .
.