题目内容
已知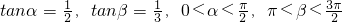 .则α+β的值是
.则α+β的值是
- A.

- B.

- C.

- D.

C
分析:先利用正切的两角和公式,把tanα和tanβ的值代入即可求得tan(α+β)的值,根据α+β的范围求得答案.
解答:tan(α+β)= =1
=1
∵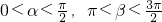
∴∵tanα<1
∴0<α<
∴π<α+β<
∴α+β=
故选C
点评:本题主要考查了正切函数的两角和公式.解题的时候注意根据角的范围判断三角函数的正负值.
分析:先利用正切的两角和公式,把tanα和tanβ的值代入即可求得tan(α+β)的值,根据α+β的范围求得答案.
解答:tan(α+β)=
 =1
=1∵
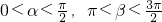
∴∵tanα<1
∴0<α<

∴π<α+β<

∴α+β=

故选C
点评:本题主要考查了正切函数的两角和公式.解题的时候注意根据角的范围判断三角函数的正负值.

练习册系列答案
相关题目
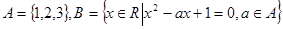 ,则
,则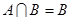 时
时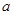 的值是
的值是 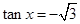 ,则函数
,则函数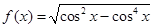 的值是
的值是
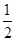 B.
B.
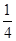 C.
C.
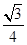 D.
D.
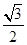
 ,则sin2x的值是( )
,则sin2x的值是( )



 ,则实数λ的值是 .
,则实数λ的值是 . ,则sin2x的值是( )
,则sin2x的值是( )


