题目内容
若函数f(x,y)=
是定义在D={(x,y)|
}上的函数,则函数f(x,y)的值域是( )
| x2+(y-3)2 |
|
A、[0,
| ||||
B、(
| ||||
C、(
| ||||
D、(
|
分析:先画出不等式组所表示的平面区域,再根据f(x,y)=
表示点(x,y)到点(0,3)的距离,
求出其中的最小值与最大值即可.
| x2+(y-3)2 |
求出其中的最小值与最大值即可.
解答: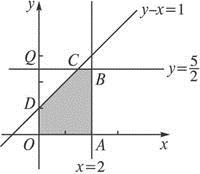 解:由题意作出定义域为如图所示的阴影部分ABCDO,
解:由题意作出定义域为如图所示的阴影部分ABCDO,
f(x,y)=
表示点P(x,y)到点Q(0,3)的距离.
且Q到直线y-x=1(即x-y+1=0)的距离d1=
=
,?
|QA|=
=
,
∴
<f(x,y)≤
.
故选D.
 解:由题意作出定义域为如图所示的阴影部分ABCDO,
解:由题意作出定义域为如图所示的阴影部分ABCDO,f(x,y)=
| x2+(y-3)2 |
且Q到直线y-x=1(即x-y+1=0)的距离d1=
| |-3+1| | ||
|
| 2 |
|QA|=
| 22+32 |
| 13 |
∴
| 2 |
| 13 |
故选D.
点评:本题主要考查二元一次不等式组、
;的几何意义.
| (x-a)2+(y-b)2 |

练习册系列答案
相关题目
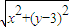 是定义在D={(x,y)|
是定义在D={(x,y)|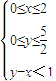 }上的函数,则函数f(x,y)的值域是( )
}上的函数,则函数f(x,y)的值域是( ) ]
]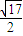 ,3]
,3]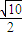 ,3]
,3]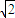 ,
,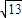 ]
]