题目内容
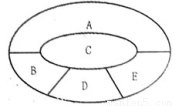
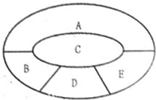 如图,某学校要用鲜花布置花圃中ABCDE五个不同区域,要求同一区域上用一种颜色的鲜花,相邻区域使用不同颜色的鲜花,现有红、黄、蓝、白、紫五种不同颜色的鲜花可供任意选择.
如图,某学校要用鲜花布置花圃中ABCDE五个不同区域,要求同一区域上用一种颜色的鲜花,相邻区域使用不同颜色的鲜花,现有红、黄、蓝、白、紫五种不同颜色的鲜花可供任意选择.(I)求恰有两个区域用红色鲜花的概率;
(II)当A、D区域同时用红色鲜花时,求布置花圃的不同方法的种数.
分析:(I)颜色相同的区域只可能是区域A、D和区域B、E,求出基本事件的总数和恰有两个区域用红色鲜花所包含的基本事件的个数即可求得.
(II)花圃中红色鲜花区域的块数可能为0,1,2.求出相应的概率即可求得分布列及期望.
(II)花圃中红色鲜花区域的块数可能为0,1,2.求出相应的概率即可求得分布列及期望.
解答: 解:(I)设M表示事件“恰有两个区域用红色鲜花”,如图:
解:(I)设M表示事件“恰有两个区域用红色鲜花”,如图:
当区域A、D同色时,共有5×4×3×1×3=180种;
当区域A、D不同色时,共有5×4×3×2×2=240种;
因此,所有基本事件总数为:180+240=420种
又因为A、D为红色时,共有4×3×3=36种;
B、E为红色时,共有4×3×3=36种;
因此,事件M包含的基本事件有:36+36=72种
所以,恰有两个区域用红色鲜花的概率P(M)=
=
.
(II)当A、D区域同时用红色鲜花时,其它区域不能用红色,
布置花圃的不同方法的种数×3×3=36种.
 解:(I)设M表示事件“恰有两个区域用红色鲜花”,如图:
解:(I)设M表示事件“恰有两个区域用红色鲜花”,如图:当区域A、D同色时,共有5×4×3×1×3=180种;
当区域A、D不同色时,共有5×4×3×2×2=240种;
因此,所有基本事件总数为:180+240=420种
又因为A、D为红色时,共有4×3×3=36种;
B、E为红色时,共有4×3×3=36种;
因此,事件M包含的基本事件有:36+36=72种
所以,恰有两个区域用红色鲜花的概率P(M)=
| 72 |
| 420 |
| 6 |
| 35 |
(II)当A、D区域同时用红色鲜花时,其它区域不能用红色,
布置花圃的不同方法的种数×3×3=36种.
点评:此题比较难,主要考查学生分析问题的能力,对学生的要求较高.求概率用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
相关题目
 (2011•邢台一模)如图,某学校要用鲜花布置花圃中ABCDE五个不同区域,要求同一区域上用一种颜色的鲜花,相邻区域使用不同颜色的鲜花,现有红、黄、蓝、白、紫五种不同颜色的鲜花可供任意选择.
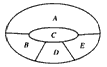
(2011•邢台一模)如图,某学校要用鲜花布置花圃中ABCDE五个不同区域,要求同一区域上用一种颜色的鲜花,相邻区域使用不同颜色的鲜花,现有红、黄、蓝、白、紫五种不同颜色的鲜花可供任意选择.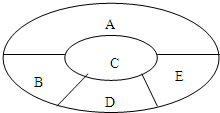 如图,某学校要用鲜花布置花圃中A,B,C,D,E五个不同区域,要求同一区域上用同一种颜色的鲜花,相邻区域使用不同的颜色的鲜花,现有红,黄,蓝,白,紫五种不同颜色的鲜花可供任意选择,记X表示花圃中用红色鲜花布置的区域的个数,则随机变量X的期望EX=
如图,某学校要用鲜花布置花圃中A,B,C,D,E五个不同区域,要求同一区域上用同一种颜色的鲜花,相邻区域使用不同的颜色的鲜花,现有红,黄,蓝,白,紫五种不同颜色的鲜花可供任意选择,记X表示花圃中用红色鲜花布置的区域的个数,则随机变量X的期望EX=