题目内容
抛掷一均匀的正方体玩具(各面分别标有数字1、2、3、4、5、6),若事件A表示“朝上一面的数是奇数”,事件B表示“朝上一面的数不超过3”,求P(A∪B).下面给出两种不同解法:
解析1:∵P(A)=![]() ,P(B)=
,P(B)=![]() ,
,
∴P(A∪B)=P(A)+P(B)=![]() .
.
解法2:A∪B这一事件包括4种结果,即出现1,2,3和5.
∴P(A∪B)=![]() .
.
请你判断解法1和解法2的正误.
解析:解法一是错误的,解法二是正确的.
错解的原因在于忽视了互斥事件的概率公式应用的前提条件,由于“朝上一面的数是奇数”与“朝上一面的数不超过3”二者不是互斥事件,即出现1或3时,事件A、B同时发生,所以不能应用P(A∪B)=P(A)+P(B)求解.
而解法二中,将A∪B分成出现“1,2,3”与“5”这两个事件,记出现“1,2,3”为事件C,出现“5”为事件D,则C与D两事件互斥,
∴P(A∪B)=P(C∪D)=P(C)+P(D)
=![]() .
.
∴解法二正确.

练习册系列答案
 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
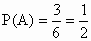 ,
,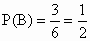 ,
,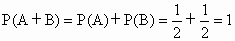 .
. .
.