题目内容
设集合D={平面向量},定义在D上的映射f,满足对任意x∈D,均有f(x)=λx(λ∈R且λ≠0).若| |=|
|=| |且
|且 、
、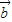 不共线,则(f(
不共线,则(f( )-f(
)-f( ))•(
))•( +
+ )=______;若A(1,2),B(3,6),C(4,8),且f(
)=______;若A(1,2),B(3,6),C(4,8),且f( )=
)=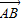 ,则λ=______.
,则λ=______.
【答案】分析:利用f(x)的定义求出f( ),
),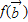 ,利用向量的运算律及向量的模的平方等于向量的平方求出;
,利用向量的运算律及向量的模的平方等于向量的平方求出;
利用向量的坐标求法求出两向量的坐标,利用f(x)的定义及已知条件列出方程求出λ.
解答:解:∵| |=|
|=| |且
|且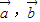 不共线,
不共线,
∴(f( )-f(
)-f( ))•(
))•(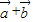 )=(λ
)=(λ -λ
-λ )•(
)•( )
)
=λ(| |2-|
|2-| |2)=0;
|2)=0;
又 ,有
,有 =λ(1,2),
=λ(1,2), ,
,
∴λ=2.
故答案为0;2
点评:本题考查的新定义题,此题型近几年高考中常出,要重视.
 ),
),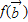 ,利用向量的运算律及向量的模的平方等于向量的平方求出;
,利用向量的运算律及向量的模的平方等于向量的平方求出;利用向量的坐标求法求出两向量的坐标,利用f(x)的定义及已知条件列出方程求出λ.
解答:解:∵|
 |=|
|=| |且
|且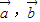 不共线,
不共线,∴(f(
 )-f(
)-f( ))•(
))•(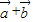 )=(λ
)=(λ -λ
-λ )•(
)•( )
)=λ(|
 |2-|
|2-| |2)=0;
|2)=0;又
 ,有
,有 =λ(1,2),
=λ(1,2), ,
,∴λ=2.
故答案为0;2
点评:本题考查的新定义题,此题型近几年高考中常出,要重视.

练习册系列答案
相关题目
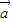 |=|
|=|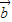 |且
|且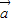 、
、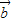 不共线,则(f(
不共线,则(f( )-f(
)-f(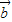 ))•(
))•(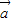 +
+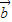 )=______;若A(1,2),B(3,6),C(4,8),且f(
)=______;若A(1,2),B(3,6),C(4,8),且f(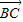 )=
)= ,则λ=______.
,则λ=______. ,则λ= .
,则λ= . ,则λ= .
,则λ= .