题目内容
(中应用举例)已知偶函数f(x)满足:f(x)=f(x+2),且当x∈[0,1]时,f(x)=sinx,其图象与直线y=
在y轴右侧的交点按横坐标从小到大依次记为P1,P2…,则
•
等于( )
| 1 |
| 2 |
| P1P3 |
| P2P4 |
| A、2 | B、4 | C、8 | D、16 |
分析:本题考查的知识是函数性质的综合应用及平面向量的数量积运算,我们可以由已知中函数f(x)满足:f(x)=f(x+2),且当x∈[0,1]时,f(x)=sinx,求出其图象与直线y=
在y轴右侧的交点P1,P2…,的关系,由于
与
同向,我们求出两个向量的模代入平面向量数量积公式,即可求解.
| 1 |
| 2 |
| P1P3 |
| P2P4 |
解答:解:依题意P1,P2,P3,P4四点共线,
与
同向,
且P1与P3,P2与P4的横坐标都相差一个周期,
所以|
|=2,
|
|=2,
•
=|
||
|=4.
故选B
| P1P3 |
| P2P4 |
且P1与P3,P2与P4的横坐标都相差一个周期,
所以|
| P1P3 |
|
| P2P4 |
| P1P3 |
| P2P4 |
| P1P3 |
| P2P4 |
故选B
点评:如果两个非量平面向量平行(共线),则它们的方向相同或相反,此时他们的夹角为0或π.当它们同向时,夹角为0,此时向量的数量积,等于他们模的积;当它们反向时,夹角为π,此时向量的数量积,等于他们模的积的相反数.如果两个向量垂直,则它们的夹角为
,此时向量的数量积等于0.
| π |
| 2 |

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
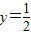 在y轴右侧的交点按横坐标从小到大依次记为P1,P2…,则
在y轴右侧的交点按横坐标从小到大依次记为P1,P2…,则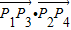 等于( )
等于( )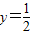 在y轴右侧的交点按横坐标从小到大依次记为P1,P2…,则
在y轴右侧的交点按横坐标从小到大依次记为P1,P2…,则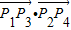 等于( )
等于( )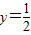 在y轴右侧的交点按横坐标从小到大依次记为P1,P2…,则
在y轴右侧的交点按横坐标从小到大依次记为P1,P2…,则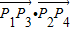 等于( )
等于( )