题目内容
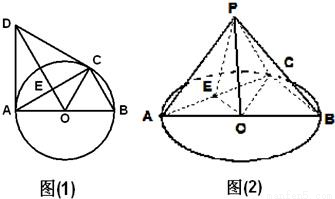
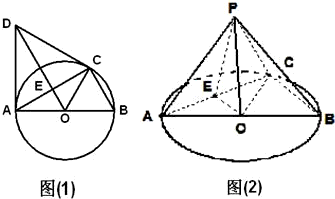 如图(1),C是直径AB=2的⊙O上一点,AD为⊙O的切线,A为切点,△ACD为等边三角形,连接DO交AC于E,以AC为折痕将△ACD翻折到图(2)的△ACP位置.
如图(1),C是直径AB=2的⊙O上一点,AD为⊙O的切线,A为切点,△ACD为等边三角形,连接DO交AC于E,以AC为折痕将△ACD翻折到图(2)的△ACP位置.
(1)求证异面直线AC和PO互相垂直;
(2)若三棱锥P-ABC的体积为 ,求二面角A-PC-B的正弦值.
,求二面角A-PC-B的正弦值.
 解:(1)证明:等边三角形△ACD中AD=DC,AD为⊙O的切线,A为切点,
解:(1)证明:等边三角形△ACD中AD=DC,AD为⊙O的切线,A为切点,∴DO⊥AC且E为AC中点 (2分)
以AC为折痕将△ACD翻折到图(2)的△ACP位置时,
仍有PE⊥AC,OE⊥AC
∴AC⊥平面PEO (4分)
∴AC⊥PO (5分)
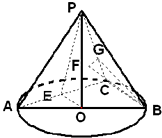
(2)过P作PK⊥EO于K,连接KA,KB,KC,
∵AC⊥平面PEO
∴AC⊥PK
∴PK⊥平面⊙O(7分)
∵PA=PC
∴KA=KC
∵图(1)中∠ADC=60°,AB=2为⊙O的直径,AD为⊙O的切线,A为切点,
∴Rt△ACB中,AC=AD=DC=AP=PC=
 ,BC=1
,BC=1∴VP-ABC=
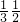 AC•BC•PK=
AC•BC•PK= PK=
PK= (8分)
(8分)∴PK=

∴KA=KC=1
∴K,O重合
∴PO⊥平面⊙O(10分)
∴PA=PB=PC=
 ,OA=OB=OC=BC=1
,OA=OB=OC=BC=1过B作BF⊥平面PAC于F,过B作BG⊥PC于G,连接FG
则PC⊥平面BFG,
∴FG⊥PC
∴∠BGF就是二面角A-PC-B的平面角(11分)
由三棱锥P-ABC的体积VP-ABC=
 =
= BF•S△PAC=
BF•S△PAC= •
• (
( )2•BF
)2•BF得BF=
 (12分)
(12分)等腰三角形PBC中,BG=
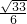
∴sin∠BGF=
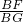 =
=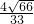
∴二面角A-PC-B的正弦值的正弦值为
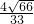 .(14分)
.(14分)分析:(1)由已知中,△ACD为等边三角形,AD为⊙O的切线,A为切点,我们易结合线面垂直的判定定理,得到翻折后AC⊥平面PEO,进而根据线面垂直的性质得到异面直线AC和PO互相垂直;
(2)过P作PK⊥EO于K,连接KA,KB,KC,由同一法我们可以证得K,O重合,过B作BF⊥平面PAC于F,过B作BG⊥PC于G,连接FG,则∠BGF就是二面角A-PC-B的平面角,利用等体积法,求出B点到平面PAC的距离BF长,即可求出二面角A-PC-B的正弦值.
点评:本题考查的知识点是二面角的平面角及求法,空间中直线与直线之间的位置关系,其中(1)的关键是熟练掌握线面垂直的判定定理及性质定理,(2)的关键是确定∠BGF就是二面角A-PC-B的平面角.

练习册系列答案
相关题目
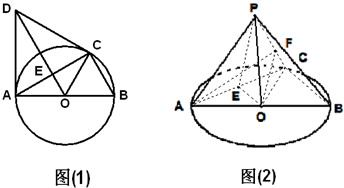 如图(1),C是直径AB=2的⊙O上一点,AD为⊙O的切线,A为切点,△ACD为等边三角形,连接DO交AC于E,以AC为折痕将△ACD翻折到图(2)的△ACP位置,点P为平面ABC外的点.
如图(1),C是直径AB=2的⊙O上一点,AD为⊙O的切线,A为切点,△ACD为等边三角形,连接DO交AC于E,以AC为折痕将△ACD翻折到图(2)的△ACP位置,点P为平面ABC外的点.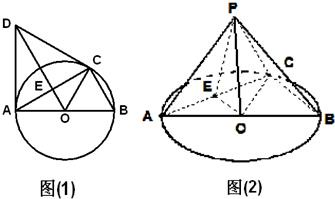 如图(1),C是直径AB=2的⊙O上一点,AD为⊙O的切线,A为切点,△ACD为等边三角形,连接DO交AC于E,以AC为折痕将△ACD翻折到图(2)的△ACP位置.
如图(1),C是直径AB=2的⊙O上一点,AD为⊙O的切线,A为切点,△ACD为等边三角形,连接DO交AC于E,以AC为折痕将△ACD翻折到图(2)的△ACP位置. ,求三棱锥P-AOF的体积.
,求三棱锥P-AOF的体积.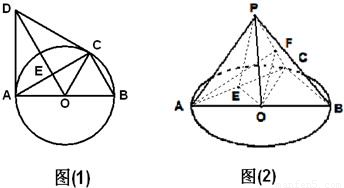
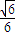 ,求二面角A-PC-B的正弦值.
,求二面角A-PC-B的正弦值.