题目内容
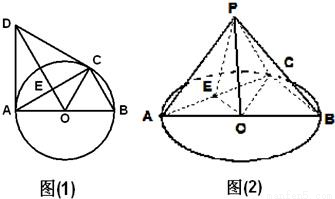
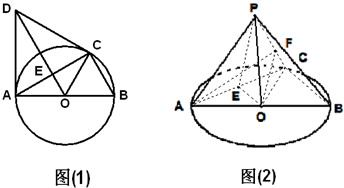 如图(1),C是直径AB=2的⊙O上一点,AD为⊙O的切线,A为切点,△ACD为等边三角形,连接DO交AC于E,以AC为折痕将△ACD翻折到图(2)的△ACP位置,点P为平面ABC外的点.
如图(1),C是直径AB=2的⊙O上一点,AD为⊙O的切线,A为切点,△ACD为等边三角形,连接DO交AC于E,以AC为折痕将△ACD翻折到图(2)的△ACP位置,点P为平面ABC外的点.(1)求证异面直线AC和PO互相垂直;
(2)若F为PC上一点,且PF=2FC,PO=
| 2 |
分析:(1)由已知中,△ACD为等边三角形,AD为⊙O的切线,A为切点,我们易结合线面垂直的判定定理,得到翻折后AC⊥平面PEO,进而根据线面垂直的性质得到异面直线AC和PO互相垂直;
(2)由已知中,△ACD为等边三角形,C是直径AB=2的⊙O上一点,F为PC上一点,且PF=2FC,PO=
,根据勾股定理,我们可得OP⊥OA,OP⊥OC,进而根据线面垂直的判定定理得到:OP⊥平面⊙O,求出三棱锥P-ABC的体积后,进一步得到三棱锥P-AOF的体积.
(2)由已知中,△ACD为等边三角形,C是直径AB=2的⊙O上一点,F为PC上一点,且PF=2FC,PO=
| 2 |
解答:证明:(1)等边三角形△ACD中AD=DC,AD为⊙O的切线,A为切点,
∴DO⊥AC且E为AC中点 (2分)
以AC为折痕将△ACD翻折到图(2)的△ACP位置时,
仍有PE⊥AC,OE⊥AC
∴AC⊥平面PEO (4分)
∴AC⊥PO (5分)
解:(2)∵PO=
,图(1)中∠DAC=60°,AB=2为⊙O的直径,AD为⊙O的切线,A为切点,
∴Rt△ACB中,AC=AD=DC=AP=PC=
,BC=1
∵OA=OB=OC=BC=1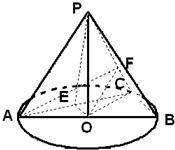
∴OA2+OP2=AP2,OC2+OP2=PC2 (8分)
∴OP⊥OA,OP⊥OC
∴OP⊥平面⊙O (10分)
∴三棱锥P-ABC的体积
VP-ABC=
•
•AB•BC•OP=
(12分)
∵F为PC上一点,且PF=2FC,
∴三棱锥P-AOF的体积
VP-AOF=
•
•VP-ABC=
(14分)
∴DO⊥AC且E为AC中点 (2分)
以AC为折痕将△ACD翻折到图(2)的△ACP位置时,
仍有PE⊥AC,OE⊥AC
∴AC⊥平面PEO (4分)
∴AC⊥PO (5分)
解:(2)∵PO=
| 2 |
∴Rt△ACB中,AC=AD=DC=AP=PC=
| 3 |
∵OA=OB=OC=BC=1

∴OA2+OP2=AP2,OC2+OP2=PC2 (8分)
∴OP⊥OA,OP⊥OC
∴OP⊥平面⊙O (10分)
∴三棱锥P-ABC的体积
VP-ABC=
| 1 |
| 3 |
| 1 |
| 2 |
| ||
| 6 |
∵F为PC上一点,且PF=2FC,
∴三棱锥P-AOF的体积
VP-AOF=
| 2 |
| 3 |
| 1 |
| 2 |
| ||
| 18 |
点评:本题考查的知识点是棱锥的体积及空间中直线与直线之间的位置关系,熟练掌握空间直线、平面之间平行及垂直的判定、性质是解答本题的关键.

练习册系列答案
相关题目
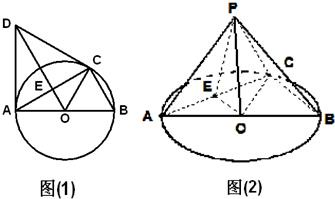 如图(1),C是直径AB=2的⊙O上一点,AD为⊙O的切线,A为切点,△ACD为等边三角形,连接DO交AC于E,以AC为折痕将△ACD翻折到图(2)的△ACP位置.
如图(1),C是直径AB=2的⊙O上一点,AD为⊙O的切线,A为切点,△ACD为等边三角形,连接DO交AC于E,以AC为折痕将△ACD翻折到图(2)的△ACP位置.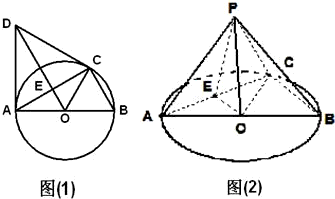 如图(1),C是直径AB=2的⊙O上一点,AD为⊙O的切线,A为切点,△ACD为等边三角形,连接DO交AC于E,以AC为折痕将△ACD翻折到图(2)的△ACP位置.
如图(1),C是直径AB=2的⊙O上一点,AD为⊙O的切线,A为切点,△ACD为等边三角形,连接DO交AC于E,以AC为折痕将△ACD翻折到图(2)的△ACP位置. ,求二面角A-PC-B的正弦值.
,求二面角A-PC-B的正弦值.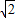 ,求三棱锥P-AOF的体积.
,求三棱锥P-AOF的体积.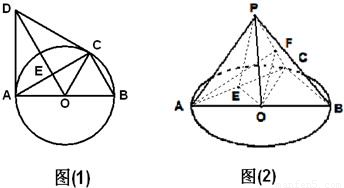
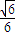 ,求二面角A-PC-B的正弦值.
,求二面角A-PC-B的正弦值.