ЬтФПФкШн
ЁОЬтФПЁПвбжЊМЏКЯM={ЃЈxЃЌyЃЉ|y=fЃЈxЃЉ}ЃЌШєЖдгкШЮвтЪЕЪ§ЖдЃЈx1 ЃЌ y1ЃЉЁЪMЃЌДцдкЃЈx2 ЃЌ y2ЃЉЁЪMЃЌЪЙx1x2+y1y2=0ГЩСЂЃЌдђГЦМЏКЯMЪЧЁАДЙжБЖдЕуМЏЁБЃЎИјГіЯТСаЫФИіМЏКЯЃК ЂйM={ЃЈxЃЌyЃЉ|y= ![]() }ЃЛ
}ЃЛ
ЂкM={ЃЈxЃЌyЃЉ|y=log2x}ЃЛ
ЂлM={ЃЈxЃЌyЃЉ|y=2xЉ2}ЃЛ
ЂмM={ЃЈxЃЌyЃЉ|y=sinx+1}ЃЎ
ЦфжаЪЧЁАДЙжБЖдЕуМЏЁБЕФађКХЪЧЃЈ ЃЉ
A.ЂйЂкЂл
B.ЂйЂкЂм
C.ЂйЂлЂм
D.ЂкЂлЂм
ЁОД№АИЁПC
ЁОНтЮіЁПНтЃКгЩЬтвтПЩЕУЃКМЏКЯMЪЧЁАДЙжБЖдЕуМЏЁБЃЌМДТњзуЃК ЧњЯпy=fЃЈxЃЉЩЯЙ§ШЮвтвЛЕугыдЕуЕФжБЯпЃЌЖМДцдкЙ§СэвЛЕугыдЕуЕФжБЯпгыжЎДЙжБЃЎ
ЂйM={ЃЈxЃЌyЃЉ|y= ![]() }ЃЌЦфЭМЯѓЯђзѓЯђгвКЭxжсЮоЯоНгНќЃЌЯђЩЯКЭyжсЮоЯоНгНќЃЌ
}ЃЌЦфЭМЯѓЯђзѓЯђгвКЭxжсЮоЯоНгНќЃЌЯђЩЯКЭyжсЮоЯоНгНќЃЌ
ОнУнКЏЪ§ЕФЭМЯѓКЭаджЪПЩжЊЃЌ
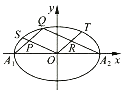
дкЭМЯѓЩЯШЮШЁвЛЕуAЃЌСЌOAЃЌЙ§дЕузїOAЕФДЙЯпOBБигыy= ![]() ЕФЭМЯѓЯрНЛЃЌ
ЕФЭМЯѓЯрНЛЃЌ
МДвЛЖЈДцдкЕуBЃЌЪЙЕУOBЁЭOAГЩСЂЃЌ
ЙЪM={ЃЈxЃЌyЃЉ|y= ![]() }ЪЧЁАДЙжБЖдЕуМЏЁБЃЎ
}ЪЧЁАДЙжБЖдЕуМЏЁБЃЎ
ЂкM={ЃЈxЃЌyЃЉ|y=log2x}ЃЌЃЈxЃО0ЃЉЃЌ
ШЁЃЈ1ЃЌ0ЃЉЃЌдђВЛДцдкЕуЃЈx2 ЃЌ log2x2ЃЉЃЈx2ЃО0ЃЉЃЌТњзу1ЁСx2+0=0ЃЌ
вђДЫМЏКЯMВЛЪЧЁАДЙжБЖдЕуМЏЁБЃЛ
ЖдгкЂлM={ЃЈxЃЌyЃЉ|y=2xЉ2}ЃЌЦфЭМЯѓЙ§ЕуЃЈ0ЃЌЉ1ЃЉЃЌЧвЯђгвЯђЩЯЮоЯобгеЙЃЌЯђзѓЯђЯТЮоЯобгеЙЃЌ
ОнжИЪ§КЏЪ§ЕФЭМЯѓКЭаджЪПЩжЊЃЌ
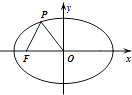
дкЭМЯѓЩЯШЮШЁвЛЕуAЃЌСЌOAЃЌЙ§дЕузїOAЕФДЙЯпOBБигыy=2xЉ2ЕФЭМЯѓЯрНЛЃЌ
МДвЛЖЈДцдкЕуBЃЌЪЙЕУOBЁЭOAГЩСЂЃЌ
ЙЪM={ЃЈxЃЌyЃЉ|y=2xЉ2}ЪЧЁАДЙжБЖдЕуМЏЁБЃЎ
ЖдгкЂмM={ЃЈxЃЌyЃЉ|y=sinx+1}ЃЌдкЭМЯѓЩЯШЮШЁвЛЕуAЃЌ
СЌOAЃЌЙ§дЕузїжБЯпOAЕФДЙЯпOBЃЌвђЮЊy=sinx+1ЕФЭМЯѓбиxжсЯђзѓЯђгвЮоЯобгеЙЃЌЧвгыxжсЯрЧаЃЌ
вђДЫжБЯпOBзмЛсгыy=sinx+1ЕФЭМЯѓЯрНЛЃЎ
ЫљвдM={ЃЈxЃЌyЃЉ|y=sinx+1}ЪЧЁАДЙжБЖдЕуМЏЁБЃЌЙЪЂмЗћКЯЃЛ
злЩЯПЩЕУЃКжЛгаЂйЂлЂмЪЧЁАДЙжБЖдЕуМЏЁБЃЎ
ЙЪбЁЃКC
ЁОПМЕуОЋЮіЁПеЦЮеУќЬтЕФецМйХаЖЯгыгІгУЪЧНтД№БОЬтЕФИљБОЃЌашвЊжЊЕРСНИіУќЬтЛЅЮЊФцЗёУќЬтЃЌЫќУЧгаЯрЭЌЕФецМйадЃЛСНИіУќЬтЮЊЛЅФцУќЬтЛђЛЅЗёУќЬтЃЌЫќУЧЕФецМйадУЛгаЙиЯЕЃЎ

 ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ
ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИ
аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИЁОЬтФПЁПЮЊСЫНтЪаУёдкЙКТђЪГЮяЪБПДгЊбјЫЕУїгыадБ№ЕФЙиЯЕЃЌЯждкЩчЛсЩЯЫцЛњбЏЮЪСЫ100УћЪаУёЃЌЕУЕНШчЯТ2ЁС2СаСЊБэЃК
ЃЈ1ЃЉЪЧЗёга95%ЕФАбЮеШЯЮЊЃКЁАадБ№гыЖСгЊбјЫЕУїгаЙиЯЕЁБЃЌВЂЫЕУїРэгЩЃЛ
ЃЈ2ЃЉАбЦЕТЪЕБИХТЪЃЌШєДгЩчЛсЩЯЕФФаадЪаУёжаЫцЛњГщШЁ3ЮЛЃЌМЧет3ЮЛжаЖСгЊбјЫЕУїЕФШЫЪ§ЮЊІЮЃЌЧѓЫцЛњБфСПІЮЕФЗжВМСаКЭЪ§бЇЦкЭћEЃЈІЮЃЉЃЎ
Фаад | ХЎад | змМЦ | |
ЖСгЊбјЫЕУї | 40 | 20 | 60 |
ВЛЖСгЊбјЫЕУї | 20 | 20 | 40 |
змМЦ | 60 | 40 | 100 |
ВЮПМЙЋЪНКЭЪ§ОнЃК ![]()
PЃЈK2Ёнk0ЃЉ | 0.10 | 0.050 | 0.025 | 0.010 |
k0 | 2.706 | 3.841 | 5.024 | 6.635 |