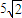题目内容

若动点P（x1，y1）在曲线y=2x2+1上移动，则点P与点（0，-l）连线中点的轨迹方程为（　　）
分析：用P点表示出中点坐标，反解出P点代入曲线方程，从而得到轨迹方程
解答：解：设点P与点（0，-1）的中点M的坐标为（x，y）
∴x=
x1+0
2
，y=
y1-1
2

即x1=2x，y1=2y+1①
∵点P在曲线y=2x2+1上移动，
∴y1=2x12+1②
将①代入②，得
2y+1=（2x）2+1
即y=4x2
故选B．
点评：本题考查轨迹方程的求法，考查中点坐标公式，考查代入法的运用，解题的关键是确定动点坐标之间的关系．
练习册系列答案
相关题目
若动点P1（x1，y1），P2（x2，y2）分别在直线l1：x-y-5=0，l2：x-y-15=0上移动，则P1P2的中点P到原点的距离的最小值是（　　）
（2012•黄冈模拟）已知坐标平面内定点和动点A（-1，0），B（1，0），M（4，0），N（0，4）和动点P（x1，y1），Q（x2，y2），若
AP
•
BP
=3，
OQ
=(
1
2
-t)
OM
+(
1
2
+t)
ON
，其中O为坐标原点，则|
PQ
|的最小值是
2
2
-2
2
2
-2
．
若动点P1（x1，y1），P2（x2，y2）分别在直线l1：x-y-5=0，l2：x-y-15=0上移动，则P1P2的中点P到原点的距离的最小值是（　　）
A．
5
2
2
B．5
2
C．
15
2
2
D．15
2
若动点P1（x1，y1），P2（x2，y2）分别在直线l1：x-y-5=0，l2：x-y-15=0上移动，则P1P2的中点P到原点的距离的最小值是（ ）
A．
B．
C．
D．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网