题目内容
 如图,以正六边形的一条对角线的两个端点F1、F2为焦点,过其余四个顶点作椭圆,则该椭圆的离心率为
如图,以正六边形的一条对角线的两个端点F1、F2为焦点,过其余四个顶点作椭圆,则该椭圆的离心率为分析:设正六边形的边长为1,则由题意可得2c=2.以线段F1F2所在的直线为x轴,以线段F1F2的中垂线为y轴,建立平面直角坐标系.则由正六边形的性质可得∠AOF1=120°,AF2=OF1=1=AO.△AOF1中,由余弦定理可得AF1 的值.再由椭圆的定义求得2a=AF1+AF2的值,由此求得离心率e=
的值
| 2c |
| 2a |
解答: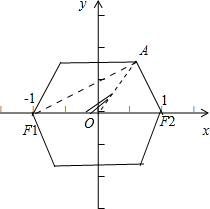 解:设正六边形的边长为1,则由题意可得2c=F1F2=2,c=1.
解:设正六边形的边长为1,则由题意可得2c=F1F2=2,c=1.
以线段F1F2所在的直线为x轴,以线段F1F2的中垂线为y轴,建立平面直角坐标系,如图所示:
作AB垂直于x轴,B为垂足,则由正六边形的性质可得∠AOF1=120°,AF2=OF1=1=AO.
△AOF1中,由余弦定理可得 AF12=AO2+OF12-2AO•OF1•cos∠AOF1=1+1-2×cos120°=3,
∴AF1=
.
再由椭圆的定义可得 2a=AF1+AF2=
+1,故离心率e=
=
=
-1,
故答案为
-1.
 解:设正六边形的边长为1,则由题意可得2c=F1F2=2,c=1.
解:设正六边形的边长为1,则由题意可得2c=F1F2=2,c=1.以线段F1F2所在的直线为x轴,以线段F1F2的中垂线为y轴,建立平面直角坐标系,如图所示:
作AB垂直于x轴,B为垂足,则由正六边形的性质可得∠AOF1=120°,AF2=OF1=1=AO.
△AOF1中,由余弦定理可得 AF12=AO2+OF12-2AO•OF1•cos∠AOF1=1+1-2×cos120°=3,
∴AF1=
| 3 |
再由椭圆的定义可得 2a=AF1+AF2=
| 3 |
| 2c |
| 2a |
| 2 | ||
|
| 3 |
故答案为
| 3 |
点评:本题主要考查椭圆的定义和简单性质的应用,正六边形的性质,属于中档题.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
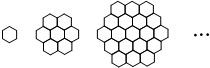 蜜蜂被认为是自然界中最杰出的建筑师,单个蜂巢可以近似地看作是一个正六边形,如图为一组蜂巢的截面图.其中第一个图有1个蜂巢,第二个图有7个蜂巢,第三个图有19个蜂巢,按此规律,以f(n)表示第n幅图的蜂巢总数.
蜜蜂被认为是自然界中最杰出的建筑师,单个蜂巢可以近似地看作是一个正六边形,如图为一组蜂巢的截面图.其中第一个图有1个蜂巢,第二个图有7个蜂巢,第三个图有19个蜂巢,按此规律,以f(n)表示第n幅图的蜂巢总数. 蜜蜂被认为是自然界中最杰出的建筑师,单个蜂巢可以近似地看作是一个正六边形,如图为一组蜂巢的截面图.其中第一个图有1个蜂巢,第二个图有7个蜂巢,第三个图有19个蜂巢,按此规律,以f(n)表示第n幅图的蜂巢总数.则f(4)=
蜜蜂被认为是自然界中最杰出的建筑师,单个蜂巢可以近似地看作是一个正六边形,如图为一组蜂巢的截面图.其中第一个图有1个蜂巢,第二个图有7个蜂巢,第三个图有19个蜂巢,按此规律,以f(n)表示第n幅图的蜂巢总数.则f(4)=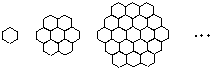 蜜蜂被认为是自然界中最杰出的建筑师,单个蜂巢可以近似地看作是一个正六边形,如图2为一组蜂巢的截面图.其中第一个图有1个蜂巢,第二个图有7个蜂巢,第三个图有19个蜂巢,按此规律,以f(n)表示第n幅图的蜂巢总数.则f(n)=
蜜蜂被认为是自然界中最杰出的建筑师,单个蜂巢可以近似地看作是一个正六边形,如图2为一组蜂巢的截面图.其中第一个图有1个蜂巢,第二个图有7个蜂巢,第三个图有19个蜂巢,按此规律,以f(n)表示第n幅图的蜂巢总数.则f(n)= 表示第
表示第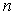 幅图的蜂巢总数.
幅图的蜂巢总数. 的值,并求
的值,并求 .
.